题目内容
探究函数f（x）=x2+
的单调性，并证明你的结论．
| 3 |
| x |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：利用函数的单调性的定义证明，本题的关键是分解因式，判断因式的符号
解答：
解：f（x1）-f（x2）=（x1-x2）（x1+x2-
）=（x1-x2）
，设x1=x2时
=0即2（x1）3-3=0解得x1=
因为函数定义域（-∞，0）∪（0，+∞），
自变量x1，x2在区间（-∞，0），（0，
），（
，+∞） 内取值时因式
符号是确定的，
而因式（x1-x2）的符号与x1，x2的大小有关系∴可以确定函数的单调区间为（-∞，0），（0，
），（
，+∞）
．证明：设x1＞x2＞
，f（x1）-f（x2）=（x1）2+
-（x2）2-
=（x1-x2）（
）
∵x1＞x2＞
∴x1-x2＞0，
＞0∴f（x1）-f（x2）＞0，即f（x1）＞f（x2）
∴函数f（x）=x2+
区间（
，+∞）上为递增函数
（2）设x1＜x2＜
，且x1≠0，x2≠0，f（x1）-f（x2）=（x1）2+
-（x2）2-
=（x1-x2）
∵x1＜x2＜∴x1-x2＜0，
＜0∴f（x1）-f（x2）＞0，即f（x1）＞f（x2）
函数f（x）=x2+
∴在区间（-∞，0），（0，
）上为减函数
| 3 |
| x1x2 |
| (x1)2x2+x1(x2)2-3 |
| x1x2 |
| (x1)2x2+x1(x2)2-3 |
| x1x2 |
| |||
| 2 |
因为函数定义域（-∞，0）∪（0，+∞），
自变量x1，x2在区间（-∞，0），（0，
| |||
| 2 |
| |||
| 2 |
| (x1)2x2+x1(x2)2-3 |
| x1x2 |
而因式（x1-x2）的符号与x1，x2的大小有关系∴可以确定函数的单调区间为（-∞，0），（0，
| |||
| 2 |
| |||
| 2 |
．证明：设x1＞x2＞
| |||
| 2 |
| 3 |
| x1 |
| 3 |
| x2 |
| (x1)2x2+x1(x2)2-3 |
| x1x2 |
∵x1＞x2＞
| |||
| 2 |
| (x1)2x2+x1(x2)2-3 |
| x1x2 |
∴函数f（x）=x2+
| 3 |
| x |
| |||
| 2 |
（2）设x1＜x2＜
| |||
| 2 |
| 3 |
| x1 |
| 3 |
| x2 |
| (x1)2x2-x1(x2)2-3 |
| x1x2 |
∵x1＜x2＜∴x1-x2＜0，
| (x1)2x2+x1(x2)2-3 |
| x1x2 |
函数f（x）=x2+
| 3 |
| x |
| |||
| 2 |
点评：本题考查了函数的单调性的定义，
练习册系列答案
相关题目
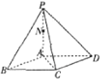如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠ABC=60°，PA⊥平面ABCD，点N是PA的中点，且PA=AB=2，点O是△PCD内（含边界）一动点，则三棱锥O-ADN的体积不小于
如图，侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中，AE=2，AC=AA1=4，∠E=60°，点B为DE中点．