题目内容
已知函数f（x）=x2-4x+c，p=f（1），q=f（4），r=f（-2），则p，q，r的大小关系是（ ）
| A、r＞p＞q |
| B、q＞p＞r |
| C、r＞q＞p |
| D、q＞r＞p |
考点：二次函数的性质
专题：
分析：通过二次函数的单调性，得出f（3）＜f（4）＜f（6），对称性得出f（1）=f（3），f（-2）=f（6），从而解决问题．
解答：
解：∵f（x）的对称轴为x=2，
∴f（1）=f（3），f（-2）=f（6），
又函数f（x）在（2，+∞）递增，
∴f（3）＜f（4）＜f（6），
即r＞q＞p，
故选：C．
∴f（1）=f（3），f（-2）=f（6），
又函数f（x）在（2，+∞）递增，
∴f（3）＜f（4）＜f（6），
即r＞q＞p，
故选：C．
点评：本题考查了二次函数的对称性，单调性，是一道基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知向量
=（6，10，-12），
=（-1，x，2），且
⊥
，则实数x的值为（ ）
| a |
| b |
| a |
| b |
A、
| ||
B、-
| ||
| C、3 | ||
| D、-3 |
已知集合A={x∈R|-1＜x＜3}，B={x∈R|-1＜x＜m+1}，若A⊆B，则实数m的取值范围是（ ）
| A、m＞2 | B、m≤2 |
| C、m≥2 | D、-2＜m＜2 |
已知函数f（x）是偶函数，且在区间[1，2]单调递减，则f（x）在区间[-2，-1]上是（ ）
| A、单调递减函数，且有最小值f（1） |
| B、单调递增函数，且有最大值f（1） |
| C、单调递减函数，且有最小值f（2） |
| D、单调递增函数，且有最大值f（2） |
sin
的值等于（ ）
| 11π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
函数f（x）=lnx+2x-6有唯一零点，其零点的范围是（ ）
| A、（1，2） |
| B、（1.5，2） |
| C、（2，3） |
| D、（3，4） |
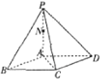如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠ABC=60°，PA⊥平面ABCD，点N是PA的中点，且PA=AB=2，点O是△PCD内（含边界）一动点，则三棱锥O-ADN的体积不小于