题目内容
下列命题中正确的是（ ）
（1）已知a，b∈R，则a=b是（a-b）+（a+b）i为纯虚数的充要条件
（2）当z是非零实数时，|z+
|≥2恒成立
（3）复数z=（1-i）3的实部和虚部都是-2
（4）设z的共轭复数为
，若z+
=4，z•
=8，则
=-i．
（1）已知a，b∈R，则a=b是（a-b）+（a+b）i为纯虚数的充要条件
（2）当z是非零实数时，|z+
| 1 |
| z |
（3）复数z=（1-i）3的实部和虚部都是-2
（4）设z的共轭复数为
. |
| z |
. |
| z |
. |
| z |
| ||
| z |
| A、（1）（2） |
| B、（1）（3） |
| C、（2）（3） |
| D、（2）（4） |
考点：复数代数形式的乘除运算,复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：（1）a，b∈R，则a=b是（a-b）+（a+b）i不一定为纯虚数；
（2）当z是非零实数时，|z+
|=|z|+
，利用基本不等式的性质即可得出；
（3）复数z=（1-i）3=-2i（1-i）=-2-2i，即可判断出其实部和虚部；
（4）设z=a+bi（a，b∈R），则共轭复数为
=a-bi，若z+
=4=2a，z•
=8=a2+b2，解得a，b．即可判断出．
（2）当z是非零实数时，|z+
| 1 |
| z |
| 1 |
| |z| |
（3）复数z=（1-i）3=-2i（1-i）=-2-2i，即可判断出其实部和虚部；
（4）设z=a+bi（a，b∈R），则共轭复数为
. |
| z |
. |
| z |
. |
| z |
解答：
解：（1）∵a，b∈R，则a=b是（a-b）+（a+b）i不一定为纯虚数，因此不正确；
（2）当z是非零实数时，|z+
|=|z|+
≥2恒成立，正确；
（3）复数z=（1-i）3=-2i（1-i）=-2-2i，其实部和虚部都是-2；
（4）设z=a+bi（a，b∈R），则共轭复数为
=a-bi，若z+
=4=2a，z•
=8=a2+b2，解得a=2，b=±2．
则
=
=
=-2i，或
=
=
=i，因此不正确．
综上可得：只有（2）（3）正确．
故选：C．
（2）当z是非零实数时，|z+
| 1 |
| z |
| 1 |
| |z| |
（3）复数z=（1-i）3=-2i（1-i）=-2-2i，其实部和虚部都是-2；
（4）设z=a+bi（a，b∈R），则共轭复数为
. |
| z |
. |
| z |
. |
| z |
则
| ||
| z |
| 2-2i |
| 2+2i |
| (1-i)2 |
| (1+i)(1-i) |
| ||
| z |
| 2+2i |
| 2-2i |
| (1+i)2 |
| (1-i)(1+i) |
综上可得：只有（2）（3）正确．
故选：C．
点评：本题综合考查了复数的有关概念及其运算性质、基本不等式的性质，考查了推理能力和技能数列，属于中档题．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
已知a、b、c为正数，且a+b+c=2，则
+
+
的最小值为（ ）
| 1 |
| a |
| 4 |
| b |
| 9 |
| c |
| A、24 | B、18 | C、12 | D、8 |
sin
的值等于（ ）
| 11π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
平行线3x-4y-3=0和6x-8y+5=0之间的距离是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
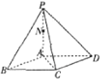如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠ABC=60°，PA⊥平面ABCD，点N是PA的中点，且PA=AB=2，点O是△PCD内（含边界）一动点，则三棱锥O-ADN的体积不小于
| ||
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
（文科）若方程
-
=1表示焦点在x轴上的椭圆，则实数m的取值范围是（ ）
| x2 |
| m+2 |
| y2 |
| m-1 |
A、（-
| ||
B、（-
| ||
| C、（-∞，1） | ||
| D、（-2，1） |
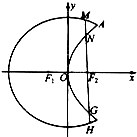我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”．如图，“盾圆C”是由椭圆