题目内容
11.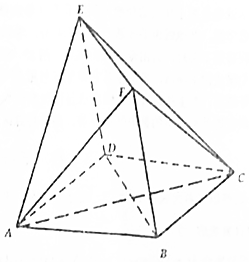 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC;
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC;(1)求证:AC⊥平面BDEF;
(2)求证:FC∥平面EAD;
(3)设AB=BF=a,求四面体A-BCF的体积.
分析 (1)设AC∩BD=O,连结FO,由AC⊥BD,AC⊥FO即可得出AC⊥平面BDEF;
(2)由BC∥AD,BF∥DE可得平面BCF∥平面EAD,从而FC∥平面EAD;
(3)证明FO⊥平面ABCD,则VA-BCF=VF-ABC=$\frac{1}{3}{S}_{△ABC}•FO$.
解答  解:(1)证明:设AC∩BD=O,连结FO,
解:(1)证明:设AC∩BD=O,连结FO,
∵四边形ABCD是菱形,
∴AC⊥BD,O是AC的中点,
又FA=FC,∴FO⊥AC,
又FO?平面BDEF,BD?平面BDEF,BD∩FO=O,
∴AC⊥平面BDEF,
(2)证明:四边形ABCD和四边形BDEF是菱形,
∴BC∥AD,BF∥DE,
又BC?平面FBC,BF?平面FBC,AD?平面EAD,
DE?平面EAD,
∴平面BCF∥平面EAD,
又FC?平面FBC,
∴FC∥平面EAD.
(3)∵四边形BDEF是菱形,∠DBF=60°,
∴△BDF是等边三角形,又O是BD的中点,
∴FO⊥OB,FO=$\frac{\sqrt{3}a}{2}$,
又FO⊥AC,OB∩AC=O,
∴FO⊥平面ABCD,
∴VA-BCF=VF-ABC=$\frac{1}{3}{S}_{△ABC}•FO$=$\frac{1}{3}×\frac{1}{2}×a×a×sin120°×\frac{\sqrt{3}a}{2}$=$\frac{{a}^{3}}{8}$.
点评 本题考查了线面平行,线面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
3.已知两个等差数列{an}和{bn}的前n项和分别为An和Bn,且$\frac{A_n}{B_n}=\frac{7n+57}{n+3}$,则使得$\frac{a_n}{b_n}$为整数的正整数n的个数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
3.对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下表:
(1)画出茎叶图;
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)数据的平均数、方差,并判断选谁参加比赛更合适?
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)数据的平均数、方差,并判断选谁参加比赛更合适?
6.高一年级有10个班,每个班有50名学生,随机编为1-50号,为了解学生在课外的兴趣爱好,要求每班第40号学生留下来进行问卷调查,则这里运用的抽样方法是( )
| A. | 分层抽样 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
3.等差数列{an}的前11项和S11=88,则a3+a6+a9=( )
| A. | 18 | B. | 24 | C. | 30 | D. | 32 |
