题目内容
20．已知等比数列{an}的公比是q，首项a1＜0，前n项和为Sn，设a1，a4，a3-a1成等差数列，若Sk＜5Sk-4，则正整数k的最大值是（ ）| A． | 4 | B． | 5 | C． | 14 | D． | 15 |
分析 运用等差数列的中项的性质，结合等比数列的定义，可得公比，再由等比数列的求和公式，以及不等式的解法，即可得到所求最大值．
解答 解：若a1，a4，a3-a1成等差数列，
可得2a4=a1+a3-a1=a3，
即有公比q=$\frac{{a}_{4}}{{a}_{3}}$=$\frac{1}{2}$，
由Sk＜5Sk-4，可得$\frac{{a}_{1}（1-\frac{1}{{2}^{k}}）}{1-\frac{1}{2}}$＜5•$\frac{{a}_{1}（1-\frac{1}{{2}^{k-4}}）}{1-\frac{1}{2}}$，
由a1＜0，化简可得1-$\frac{1}{{2}^{k}}$＞5-$\frac{5}{{2}^{k-4}}$，
即为2k＜$\frac{79}{4}$，可得正整数k的最大值为k为4．
故选：A．
点评 本题考查等比数列的求和公式和等差数列的中项的性质，考查化简整理的运算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
11．
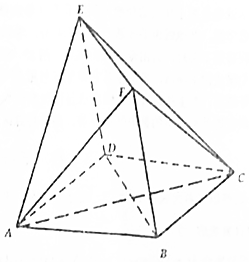如图，四边形ABCD与BDEF均为菱形，∠DAB=∠DBF=60°，且FA=FC；
（1）求证：AC⊥平面BDEF；
（2）求证：FC∥平面EAD；
（3）设AB=BF=a，求四面体A-BCF的体积．
如图，四边形ABCD与BDEF均为菱形，∠DAB=∠DBF=60°，且FA=FC；（1）求证：AC⊥平面BDEF；
（2）求证：FC∥平面EAD；
（3）设AB=BF=a，求四面体A-BCF的体积．
11．已知tanα=3，则2sin2α-sinαcosα+cos2α的值等于（ ）
| A． | $\frac{8}{9}$ | B． | $\frac{7}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{8}{5}$ |
8．
如图所示，两个非共线向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为θ，N为OB中点，M为OA上靠近A的三等分点，点C在直线MN上，且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$（x、y∈R），则x2+y2的最小值为（ ）
如图所示，两个非共线向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为θ，N为OB中点，M为OA上靠近A的三等分点，点C在直线MN上，且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$（x、y∈R），则x2+y2的最小值为（ ）| A． | $\frac{4}{25}$ | B． | $\frac{2}{5}$ | C． | $\frac{4}{9}$ | D． | $\frac{2}{3}$ |
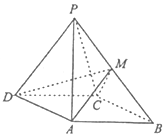如图，四棱锥P-ABCD中，侧面PDC是正三角形，底面ABCD是边长为2$\sqrt{3}$的菱形，∠DAB=120°，且侧面PDC与底面垂直，M为PB的中点．