已知直线5x+12y+a=0与圆x2-2x+y2=0相切.求a的值．题目和参考答案——青夏教育精英家教网—

题目内容

18．已知直线5x+12y+a=0与圆x²-2x+y²=0相切，求a的值．

分析根据直线与圆相切的性质可知圆心直线的距离为半径，先把圆的方程整理的标准方程求得圆心和半径，在利用点到直线的距离求得圆心到直线的距离为半径，求得答案．

解答解：整理圆的方程为（x-1）²++y²=1
故圆的圆心为（1，0），半径为1
∵直线与圆相切
∴圆心到直线的距离为半径
即$\frac{|5+a|}{\sqrt{25+144}}$=1，求得a=8或a=-18．

点评本题主要考查了直线与圆的位置关系．解题的过程充分利用数形结合的思想和直线与圆相切的性质．

练习册系列答案

9．已知函数f（x）=-4cos²x+4$\sqrt{3}$asinxcosx+2，若f（x）的图象关于点（$\frac{π}{12}$，0）对称．
（1）求实数a，并求出f（x）的单调减区间；
（2）求f（x）的最小正周期，并求f（x）在[-$\frac{π}{4}$，$\frac{π}{6}$]上的值域．

6．直线x+y=5与直线x-y=1交点坐标是（　　）

13．圆心在原点，半径为5的圆的方程是x²+y²=25．

3．若一个高为4，底面边长为2的正四棱锥的顶点都在同一个球面上，则该球的表面积为（　　）

10．已知两点A（-2，0），B（0，2），点C是圆x²+y²-2x=0上任意一点，则△ABC面积的最大值是（　　）

$3-\frac{{\sqrt{2}}}{2}$

D．

$\frac{{3-\sqrt{2}}}{2}$

7．在等差数列{a_n}中，其前n项和记为S_n，
（1）若S₁₀₁=0，则a₅₁=0；
（2）若6S₅-5S₃=5，则a₄=$\frac{1}{3}$．

8．

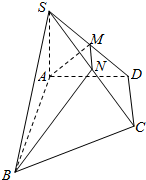如图，在直角梯形ABCD中，∠BAD=∠ADC=90°，CD=DA=a，AB=2a，SA⊥平面ABCD，且SA=a
（1）求证：△SAD，△SAB，△SCB，△SDC都是直角三角形；
（2）在SD上取点M，SC交平面ABM于N，求证；四边形ABNM为直角梯形．

试题分类