题目内容
10.已知两点A(-2,0),B(0,2),点C是圆x2+y2-2x=0上任意一点,则△ABC面积的最大值是( )| A. | 3-$\sqrt{2}$ | B. | $3+\sqrt{2}$ | C. | $3-\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{3-\sqrt{2}}}{2}$ |
分析 求出圆上动点C到直线AB的最大距离,代入三角形面积公式,可得答案.
解答 解:∵A(-2,0),B(0,2),
∴直线AB的方程为:$\frac{x}{-2}+\frac{y}{2}=1$,即x-y+2=0,且AB=2$\sqrt{2}$,
圆x2+y2-2x=0的圆心坐标为(1,0),半径为1,
则圆心到直线的距离d=$\frac{3}{\sqrt{2}}$,
故C到AB的距离距离为:$\frac{3}{\sqrt{2}}$+1,
此时△ABC面积取最大值$\frac{1}{2}$×2$\sqrt{2}$×$\frac{3}{\sqrt{2}}$+1=3+$\sqrt{2}$,
故选:B
点评 本题考查的知识点是直线与圆的位置关系,点到直线的距离公式,三角形面积公式,难度不大,属于基础题目.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
1.$若log_a^{\;}\frac{2}{3}<1,(a>0且a≠1)$,则a的取值范围是( )
| A. | ($\frac{2}{3}$,1) | B. | (0,$\frac{2}{3}$)∪(1,+∞) | C. | (1,+∞) | D. | (0,$\frac{2}{3}$)∪($\frac{2}{3}$,+∞) |
5.已知ab≠0,点M(a,b)是圆x2+y2=r2内一点,直线l的方程是ax+by=r2,则下列结论正确的是( )
| A. | l与圆相交 | B. | l与圆相切 | C. | l与圆相离 | D. | 不确定 |
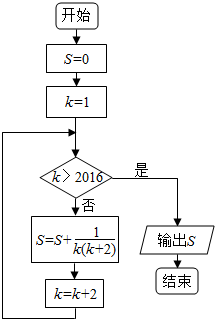
20.执行下列程序框图,则输出结果为( )


| A. | 413 | B. | 404 | C. | 397 | D. | 407 |