题目内容
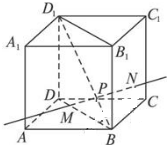 如图,动点P在正方体ABCD-A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,△BMN的面积是y,则函数y=f(x)的图象大致是( )
如图,动点P在正方体ABCD-A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,△BMN的面积是y,则函数y=f(x)的图象大致是( )A、 |
B、 |
C、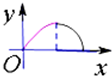 |
D、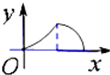 |
考点:棱柱的结构特征,函数的图象与图象变化
专题:函数的性质及应用,空间位置关系与距离
分析:根据题意和正方体的特征,分析点P动的过程中,x随着y变化情况以及变化速度,再对照选项中的图形选出.
解答:
解:由题意知,MN⊥平面BB1D1D,其轨迹经过B,D1和侧棱AA1,CC1的中点E,F,

设对角线BD1的中点为O,

则当P点位于线段BO上时,
当BP增大时,MN随BP线性增加,则函数y=f(x)的图象应为开口朝上二次函数图象递增的一部分,故可排除A,C,
当P点位于线段OD1上时,

当BP增大时,MN随(BD1-BP)线性变化,则函数y=f(x)的图象应为开口朝下二次函数图象递减的一部分,故可排除B,
故选:D

设对角线BD1的中点为O,

则当P点位于线段BO上时,
当BP增大时,MN随BP线性增加,则函数y=f(x)的图象应为开口朝上二次函数图象递增的一部分,故可排除A,C,
当P点位于线段OD1上时,

当BP增大时,MN随(BD1-BP)线性变化,则函数y=f(x)的图象应为开口朝下二次函数图象递减的一部分,故可排除B,
故选:D
点评:本题考查了函数图象的变化,根据几何体的特征和条件进行分析两个变量的变化情况,再用图象表示出来,考查了作图和读图能力.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
函数y=(cosx+sinx)•(cosx-sinx)的最小正周期是( )
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
不等式|x|>
的解集是( )
| 1 |
| x |
| A、(-∞,-1)∪(1,+∞) |
| B、(-∞,0)∪(1,+∞) |
| C、(-1,0)∪(1,+∞) |
| D、(-∞,-1)∪(0,1) |
函数f(x)=
的图象大致是( )
| x3-3 |
| ex |
A、 |
B、 |
C、 |
D、 |
已知△ABC的内角A、B、C的对边分别为a、b、c,若a2-c2=b2+bc,则A=( )
| A、30° | B、60° |
| C、120° | D、150° |
cos20°sin65°-sin20°cos65°=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|