题目内容
已知函数f(x)=
是R上的减函数,求实数a的取值范围 .
|
考点:分段函数的应用
专题:函数的性质及应用
分析:由一次函数和指数函数的性质,先求出各个分段上的a的取值范围,再综合得出结论.
解答:
解:当x<1时,f(x)=(a-2)x+4a,
∴f′(x)=a-2<0,解得:a<2,
当x≥1时,f(x)=ax,0<a<1时,f(x)是减函数,
且x=1时,a≤a-2+4a,解得:a≥
,
综上:
≤a<1;
故答案为:[
,1).
∴f′(x)=a-2<0,解得:a<2,
当x≥1时,f(x)=ax,0<a<1时,f(x)是减函数,
且x=1时,a≤a-2+4a,解得:a≥
| 1 |
| 2 |
综上:
| 1 |
| 2 |
故答案为:[
| 1 |
| 2 |
点评:本题考察了分段函数的应用,一次函数以及指数函数的性质,是一道基础题.

练习册系列答案
相关题目
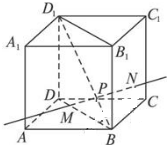 如图,动点P在正方体ABCD-A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,△BMN的面积是y,则函数y=f(x)的图象大致是( )
如图,动点P在正方体ABCD-A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,△BMN的面积是y,则函数y=f(x)的图象大致是( )A、 |
B、 |
C、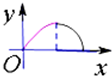 |
D、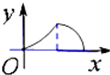 |
将函数y=5sin3x的图象向左平移π个单位,得到的图象的解析式是( )
A、y=5sin(3x+
| ||
B、y=5sin(3x-
| ||
| C、y=5sin3x | ||
| D、y=-5sin3x |