题目内容
函数y=(cosx+sinx)•(cosx-sinx)的最小正周期是( )
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
考点:二倍角的余弦,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:利用二倍角的余弦公式化简函数的解析式为y=cos2x,由此可得函数的最小正周期.
解答:
解:∵函数y=(cosx+sinx)•(cosx-sinx)=cos2x-sin2x=cos2x,
故函数的最小正周期为
=π,
故选:B.
故函数的最小正周期为
| 2π |
| 2 |
故选:B.
点评:本题主要考查二倍角的余弦公式,三角函数的周期性和求法,属于基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
若a,b,c为实数,则下列不等式恒成立的是( )
| A、若a>b,则ac2>bc2 | ||||
B、若a>b,则
| ||||
| C、若a<b,则a2<b2 | ||||
| D、若a+c>b+c,则a>b |
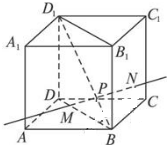 如图,动点P在正方体ABCD-A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,△BMN的面积是y,则函数y=f(x)的图象大致是( )
如图,动点P在正方体ABCD-A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,△BMN的面积是y,则函数y=f(x)的图象大致是( )A、 |
B、 |
C、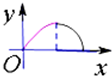 |
D、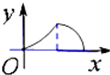 |
对于集合A={x|x=3m+2n,m,n∈Z},B={x|x=3m+8n,m,n∈Z},下列说法中正确的是( )
| A、A?B | B、A?B |
| C、A?Z,B?Z | D、A=B |
已知a、b∈R,“a<b”是“2a<3b”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
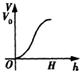
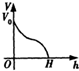
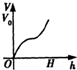
 一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )
一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )