题目内容
cos20°sin65°-sin20°cos65°=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
考点：两角和与差的正弦函数
专题：计算题,三角函数的求值
分析：逆用两角差的正弦公式可以化成sin（65°-20°），然后求值．
解答：
解：cos20°sin65°-sin20°cos65°
=sin（65°-20°）
=sin45°
=
故选C．
=sin（65°-20°）
=sin45°
=
| ||
| 2 |
故选C．
点评：本题考查了两角差的正弦公式的逆用，解题的关键是要对公式的形式比较熟悉．
练习册系列答案
相关题目
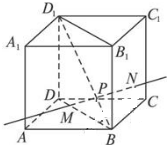如图，动点P在正方体ABCD-A1B1C1D1的对角线BD1上，过点P作垂直于平面BB1D1D的直线，与正方体表面相交于M，N．设BP=x，△BMN的面积是y，则函数y=f（x）的图象大致是（ ）A、 |
B、 |
C、 |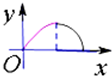
D、 |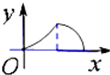
将函数y=5sin3x的图象向左平移π个单位，得到的图象的解析式是（ ）
A、y=5sin（3x+
| ||
B、y=5sin（3x-
| ||
| C、y=5sin3x | ||
| D、y=-5sin3x |
已知cosα=-
，sinα=
，那么α的终边所在的象限为（ ）
| 3 |
| 5 |
| 4 |
| 5 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知a、b∈R，“a＜b”是“2a＜3b”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
在本市某机关今年的公务员考试成绩中随机抽取25名考生的笔试成绩，并分成5组，得到频率分布直方图如图所示．已知成绩落在第2组[110，120）内的人数为8人．