题目内容
对于任意α∈R,下列等式中恒成立的个数有 个.
A.sin(2π-α)=sinα
B.cos(-α)=cosα
C.cos(π-α)=cos(2π+α)
D.cos(
-α)=-cosα.
A.sin(2π-α)=sinα
B.cos(-α)=cosα
C.cos(π-α)=cos(2π+α)
D.cos(
| π |
| 2 |
考点:诱导公式的作用
专题:三角函数的求值
分析:结合诱导公式,进行逐一验证即可.
解答:
解:对于A:sin(2π-α)=-sinα,故A错;
对于B:cos(-α)=cosα 正确;
对于C:cos(π-α)=-cosα,cos(2π+α)=cosα,C错误;
对于D:cos(
-α)=sinα≠-cosα.D错误.
故答案为:1.
对于B:cos(-α)=cosα 正确;
对于C:cos(π-α)=-cosα,cos(2π+α)=cosα,C错误;
对于D:cos(
| π |
| 2 |
故答案为:1.
点评:本题重点考查了诱导公式及其应用,属于基础题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
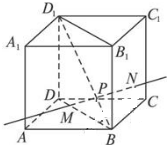 如图,动点P在正方体ABCD-A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,△BMN的面积是y,则函数y=f(x)的图象大致是( )
如图,动点P在正方体ABCD-A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,△BMN的面积是y,则函数y=f(x)的图象大致是( )