题目内容
已知△ABC的内角A、B、C的对边分别为a、b、c,若a2-c2=b2+bc,则A=( )
| A、30° | B、60° |
| C、120° | D、150° |
考点:余弦定理
专题:计算题,解三角形
分析:原式可变形为
=-
,由余弦定理可得cosA,由此可求A.
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
解答:
解:a2-c2=b2+bc,可化为b2+c2-a2=-bc,
两边同除以2bc,得
=-
,
由余弦定理,得cosA=-
,
∴A=120°,
故选:C.
两边同除以2bc,得
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
由余弦定理,得cosA=-
| 1 |
| 2 |
∴A=120°,
故选:C.
点评:该题考查余弦定理及其应用,对余弦定理的内容要熟练,会“正用、逆用、变形用”.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
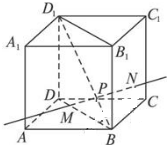 如图,动点P在正方体ABCD-A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,△BMN的面积是y,则函数y=f(x)的图象大致是( )
如图,动点P在正方体ABCD-A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,△BMN的面积是y,则函数y=f(x)的图象大致是( )A、 |
B、 |
C、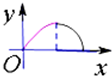 |
D、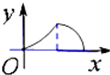 |
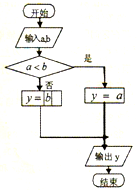 定义某种运算※,a※b的运算原理如图所示,设f(x)=(0※x)x-(2※x),则f(x)在区间[-2,2]上的最小值为( )
定义某种运算※,a※b的运算原理如图所示,设f(x)=(0※x)x-(2※x),则f(x)在区间[-2,2]上的最小值为( )| A、-2 | B、-4 | C、-6 | D、0 |
设a∈R,若函数y=ex+3ax,x∈R有大于零的极值点,则( )
| A、a>-3 | ||
| B、a<-3 | ||
C、a>-
| ||
D、a<-
|
将函数y=5sin3x的图象向左平移π个单位,得到的图象的解析式是( )
A、y=5sin(3x+
| ||
B、y=5sin(3x-
| ||
| C、y=5sin3x | ||
| D、y=-5sin3x |
已知cosα=-
,sinα=
,那么α的终边所在的象限为( )
| 3 |
| 5 |
| 4 |
| 5 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
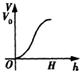
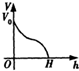
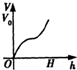
 一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )
一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )