题目内容
不等式|x|＞
的解集是（ ）
| 1 |
| x |
| A、（-∞，-1）∪（1，+∞） |
| B、（-∞，0）∪（1，+∞） |
| C、（-1，0）∪（1，+∞） |
| D、（-∞，-1）∪（0，1） |
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：由题意可得，x＜0，或
，由此解得x的范围．
|
解答：
解：由不等式|x|＞
可得 x＜0，或
，解得 x＜0，或x＞1，
故选：B．
| 1 |
| x |
|
故选：B．
点评：本题主要考查绝对值不等式的解法，体现了转化、分类讨论的数学思想，属于基础题．
练习册系列答案
相关题目
已知a、b∈R，a+bi是虚数的充分必要条件是（ ）
| A、ab≠0 | B、a≠0 |
| C、b≠0 | D、a=0且b≠0 |
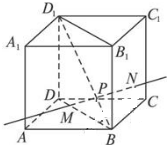如图，动点P在正方体ABCD-A1B1C1D1的对角线BD1上，过点P作垂直于平面BB1D1D的直线，与正方体表面相交于M，N．设BP=x，△BMN的面积是y，则函数y=f（x）的图象大致是（ ）A、 |
B、 |
C、 |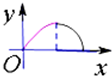
D、 |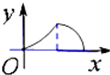
已知tanα=-
，sinβ=
，β∈（
，π），则tan（2α-β）=（ ）
| 1 |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
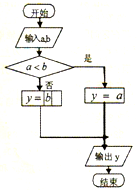定义某种运算※，a※b的运算原理如图所示，设f（x）=（0※x）x-（2※x），则f（x）在区间[-2，2]上的最小值为（ ）| A、-2 | B、-4 | C、-6 | D、0 |
设a∈R，若函数y=ex+3ax，x∈R有大于零的极值点，则（ ）
| A、a＞-3 | ||
| B、a＜-3 | ||
C、a＞-
| ||
D、a＜-
|