题目内容
数列{an}中,a1=3,an+1=3an-4(n∈N*),则通项公式an= .
考点:数列递推式
专题:等差数列与等比数列
分析:由题意知an+1-2=3(an-2),判断{an-2}是等比数列,由此求出通项公式.
解答:
解:∵数列{an}中,a1=3,an+1=3an-4(n∈N*),∴an+1-2=3(an-2),
∵a1-2=1,
∴{an-2}是公比为3,首项是1的等比数列,即an-2=1×3n-1,
an=3n-1+2.
故答案为:3n-1+2.
∵a1-2=1,
∴{an-2}是公比为3,首项是1的等比数列,即an-2=1×3n-1,
an=3n-1+2.
故答案为:3n-1+2.
点评:本题考查数列的性质和应用,合理地进行构造新数列是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
不等式x2-2x+5≥a2-3a对任意实数x恒成立,则实数a的取值范围为( )
| A、[-1,4] |
| B、(-∞,-2]∪[5,+∞) |
| C、(-∞,-1]∪[4,+∞) |
| D、[-2,5] |
若y=f(2x)的图象关于直线x=
和x=
(b>a)对称,则f(x)的一个周期为( )
| a |
| 2 |
| b |
| 2 |
A、
| ||
| B、2(b-a) | ||
C、
| ||
| D、4(b-a) |
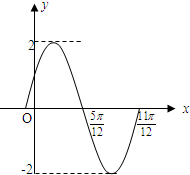 已知函数f(x)=A(sinωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示.
已知函数f(x)=A(sinωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示.