题目内容
10.甲乙两人相约上午8点到9点在某地会面,先到者等候另一个人20分钟,过时离去,则甲乙两人能够会面的概率是( )| A. | $\frac{1}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{3}$ |
分析 由题意知本题是一个几何概型,试验包含的所有事件是Ω={(x,y)|8<x<9,8<y<9},做出事件对应的集合表示的面积,写出满足条件的事件是A={(x,y)|8<x<9,8<y<9,|x-y|<$\frac{20}{60}$},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.
解答 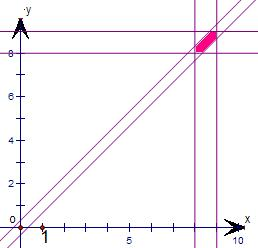 解:由题意知本题是一个几何概型,
解:由题意知本题是一个几何概型,
设事件A为“两人能会面”,
试验包含的所有事件是
Ω={(x,y)|8<x<9,8<y<9},
并且事件对应的集合表示的面积是S=1,
满足条件的事件是
A={(x,y)|8<x<9,8<y<9,|x-y|<$\frac{20}{60}$}
所以事件对应的集合表示的图中阴影部分,
其面积是1-2×$\frac{1}{2}×\frac{2}{3}×\frac{2}{3}$=$\frac{5}{9}$,
根据几何概型概率公式得到P=$\frac{5}{9}$.
故选:C.
点评 本题是一个几何概型,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.

练习册系列答案
相关题目
20.某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据,则其线性回归直线方程是y=6.5x+17.5
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
1.确定结论“X与Y有关系”的可信度为99.9%时,则随机变量k2的观测值k必须( )
| A. | 大于10.828 | B. | 小于7.829 | C. | 小于6.635 | D. | 大于2.706 |
15.设${({5x-\frac{1}{{\sqrt{x}}}})^n}$的展开式的二项式系数和为64,则展开式中常数项为( )
| A. | 375 | B. | -375 | C. | 15 | D. | -15 |
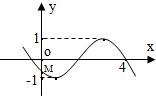 已知函数f(x)=Asin(ωx+φ)(x∈R),且A>0,ω>0,-π≤φ≤0.若f(x)的部分图象如图,且与y轴交点M(0,-$\frac{{\sqrt{2}}}{2}$),则ω+φ=-$\frac{5π}{16}$.
已知函数f(x)=Asin(ωx+φ)(x∈R),且A>0,ω>0,-π≤φ≤0.若f(x)的部分图象如图,且与y轴交点M(0,-$\frac{{\sqrt{2}}}{2}$),则ω+φ=-$\frac{5π}{16}$.