题目内容
19.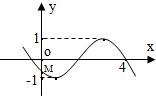 已知函数f(x)=Asin(ωx+φ)(x∈R),且A>0,ω>0,-π≤φ≤0.若f(x)的部分图象如图,且与y轴交点M(0,-$\frac{{\sqrt{2}}}{2}$),则ω+φ=-$\frac{5π}{16}$.
已知函数f(x)=Asin(ωx+φ)(x∈R),且A>0,ω>0,-π≤φ≤0.若f(x)的部分图象如图,且与y轴交点M(0,-$\frac{{\sqrt{2}}}{2}$),则ω+φ=-$\frac{5π}{16}$.
分析 由函数的图象的顶点坐标求出A,由图象和y轴的交点坐标求出φ,由五点法作图求出ω的值,从而求得ω+φ的值.
解答 解:根据函数f(x)=Asin(ωx+φ)(x∈R,且A>0,ω>0,-π≤φ≤0)的部分图象,
可得A=1,把点M的坐标代入,求得sinφ=-$\frac{\sqrt{2}}{2}$,结合图象可得 φ=-$\frac{3π}{4}$,f(x)=sin(ωx-$\frac{3π}{4}$).
再结合五点法作图可得ω•4-$\frac{3π}{4}$=π,求得ω=$\frac{7π}{16}$,∴ω+φ=$\frac{7π}{16}$-$\frac{3π}{4}$=-$\frac{5π}{16}$.
故答案为:$-\frac{5π}{16}$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由图象和y轴的交点坐标求出 φ,由五点法作图求出ω的值,属于基础题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
10.甲乙两人相约上午8点到9点在某地会面,先到者等候另一个人20分钟,过时离去,则甲乙两人能够会面的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{3}$ |
9.在一次实验中,测得(x,y)的四组值分别是A(1,2),B(2,2.8),C(3,4),D(4,5.2),则y与x之间的回归直线方程为( )
| A. | $\stackrel{∧}{y}$=2x+1 | B. | $\stackrel{∧}{y}$=x+2 | C. | $\stackrel{∧}{y}$=x+1 | D. | $\stackrel{∧}{y}$=x-1 |
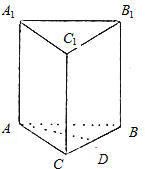 如图,在直三棱柱ABC-A1B1C1中,AB=BC=AC=AA1=1,D是BC的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=AC=AA1=1,D是BC的中点.