题目内容
18.对于实数x,用[x]表示不超过x的最大整数,如[0.41]=0,[7.28]=7,若n为正整数,an=[$\frac{n}{3}$],Sn为数列{an}的前n项和,S3n=$\frac{3}{2}{n}^{2}-\frac{n}{2}$.分析 利用n∈N*,an=[$\frac{n}{3}$],可得S3n=3[0+1+2+…+(n-1)]+n,由此可得结论.
解答 解:∵n∈N*,an=[$\frac{n}{3}$],
∴n=3k,k∈N*时,a3k=k;n=3k+1,k∈N时,a3k+1=k;n=3k+2,k∈N时,a3k+2=k.
∴S3n=3[0+1+2+…+(n-1)]+n=$3×\frac{[1+(n-1)](n-1)}{2}+n=\frac{3{n}^{2}}{2}-\frac{n}{2}$.
故答案为:$\frac{3}{2}{n}^{2}-\frac{n}{2}$.
点评 本题主要考查数列与函数的综合运用,主要涉及了数列的推导与归纳,是新定义题,应熟悉定义,将问题转化为已知去解决,是中档题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
13.函数f(x)=(${\frac{1}{2}}$)${\;}^{{x^2}-2x+2}}$的值域是( )
| A. | (0,$\frac{1}{2}$] | B. | (-∞,$\frac{1}{2}$] | C. | (-∞,2] | D. | [$\frac{1}{2}$,+∞) |
10.甲乙两人相约上午8点到9点在某地会面,先到者等候另一个人20分钟,过时离去,则甲乙两人能够会面的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{3}$ |
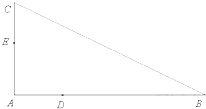 如图,△ABC中∠A=90°,D,E分别为边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.
如图,△ABC中∠A=90°,D,E分别为边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.