题目内容
15.设${({5x-\frac{1}{{\sqrt{x}}}})^n}$的展开式的二项式系数和为64,则展开式中常数项为( )| A. | 375 | B. | -375 | C. | 15 | D. | -15 |
分析 由题意可得:2n=64,解得n=6.再利用$(5x-\frac{1}{\sqrt{x}})^{6}$的通项公式即可得出.
解答 解:由题意可得:2n=64,解得n=6.
∴$(5x-\frac{1}{\sqrt{x}})^{6}$的通项公式为:Tr+1=${∁}_{6}^{r}$(5x)6-r$(-\frac{1}{\sqrt{x}})^{r}$=(-1)r56-r${∁}_{6}^{r}$${x}^{6-\frac{3}{2}r}$,
令6-$\frac{3}{2}r$=0,解得r=4.
∴展开式中常数项为T5=52×${∁}_{6}^{4}$=375.
故选:A.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
10.甲乙两人相约上午8点到9点在某地会面,先到者等候另一个人20分钟,过时离去,则甲乙两人能够会面的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{3}$ |
5.若函数y=f(x+1)是偶函数,则函数y=f(x)的图象的对称轴方程是( )
| A. | x=1 | B. | x=-1 | C. | x=2 | D. | x=-2 |
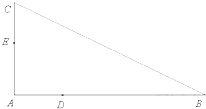 如图,△ABC中∠A=90°,D,E分别为边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.
如图,△ABC中∠A=90°,D,E分别为边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.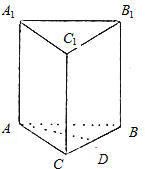 如图,在直三棱柱ABC-A1B1C1中,AB=BC=AC=AA1=1,D是BC的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=AC=AA1=1,D是BC的中点.