题目内容
(Ⅰ)计算π0+2-2×(
)-
-(0.01)0.5;
(Ⅱ)计算2log510+log50.25.
| 9 |
| 4 |
| 1 |
| 2 |
(Ⅱ)计算2log510+log50.25.
考点:对数的运算性质,根式与分数指数幂的互化及其化简运算
专题:函数的性质及应用
分析:(Ⅰ)利用分数指数幂的去处法则求解.
(Ⅱ)利用对数的去处法则求解.
(Ⅱ)利用对数的去处法则求解.
解答:
解:(Ⅰ)π0+2-2×(
)-
-(0.01)0.5;
=1+
×[(
)-1]
-0.01
=1+
×[
]
-(
)
=1+
×
-
=
.…(6分)
(Ⅱ)2log510+log50.25
=log5100+log50.25
=log525=2.
| 9 |
| 4 |
| 1 |
| 2 |
=1+
| 1 |
| 22 |
| 9 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
=1+
| 1 |
| 4 |
| 4 |
| 9 |
| 1 |
| 2 |
| 1 |
| 100 |
| 1 |
| 2 |
=1+
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 10 |
| 16 |
| 15 |
(Ⅱ)2log510+log50.25
=log5100+log50.25
=log525=2.
点评:本题考查指数式和对数式化简求值,是基础题,解题时要注意运算法则的合理运用.

练习册系列答案
相关题目
已知点(
,
)在幂函数y=f(x)的图象上,则f(x)的表达式是( )
| ||
| 3 |
| ||
| 9 |
A、f(x)=
| ||
| B、f(x)=x3 | ||
| C、f(x)=x-2 | ||
D、f(x)=(
|
若sin(x-
)=
,则cos(
-2x)=( )
| π |
| 6 |
| 1 |
| 3 |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知等差数列{an}满足an>0,则
的最小值为( )
| (a1+a10)2 |
| a5a6 |
| A、1 | B、4 | C、6 | D、8 |

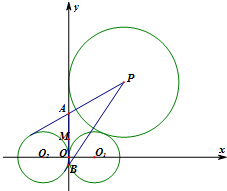 如图,在y轴右侧的动圆⊙P与⊙O1:(x-1)2+y2=1外切,并与y轴相切.
如图,在y轴右侧的动圆⊙P与⊙O1:(x-1)2+y2=1外切,并与y轴相切. 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC、BD交于点G.
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC、BD交于点G.