Question

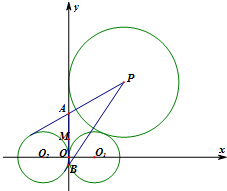如图，在y轴右侧的动圆⊙P与⊙O₁：（x-1）²+y²=1外切，并与y轴相切．
（Ⅰ）求动圆的圆心P的轨迹Γ的方程；
（Ⅱ）过点P作⊙O₂：（x+1）²+y²=1的两条切线，分别交y轴于A，B两点，设AB中点为M（0，m）．求m的取值范围．

Answer 1

考点：轨迹方程,直线与圆的位置关系

专题：综合题,圆锥曲线的定义、性质与方程

分析：（Ⅰ）利用抛物线的定义，求动圆的圆心P的轨迹Γ的方程；
（Ⅱ）求出（x+1）²+y²=1的圆心（-1，0）到切线的距离，两边平方并整理，利用韦达定理，确定A，B两点的纵坐标，即可确定m的取值范围．

解答： 解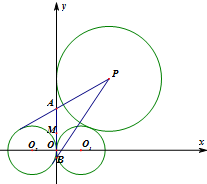：（Ⅰ）由题意，点P到点（1，0）的距离等于它到直线x=-1的距离，
故Γ是抛物线，方程为y²=4x（x≠0）．…（5分）
（Ⅱ）设P(

t2

4

，t)（t≠0），切线斜率为k，
则切线方程为y-t=k(x-

t2

4

)，即kx-y+t-

kt2

4

=0．…（6分）
由题意，（x+1）²+y²=1的圆心（-1，0）到切线的距离

|-k+t- kt2 4 |

1+k2

=1，…（8分）
两边平方并整理得：t²（t²+8）k²-8t（t²+4）k+t²-1=0．…（9分）
该方程的两根k₁，k₂就是两条切线的斜率，由韦达定理：k1+k2=

8t(t2+4)

t2(t2+8)

．  ①…（11分）
另一方面，在y-t=k1(x-

t2

4

)，y-t=k2(x-

t2

4

)中，
令x=0可得A，B两点的纵坐标y1=t-

t2

4

k1，y2=t-

t2

4

k2，
故m=

y1+y2

2

=t-

t2

8

(k1+k2)，②…（13分）
将①代入②，得m=

4t

t2+8

=

4

t+ 8 t

，…（14分）
故m的取值范围是-

2

2

≤m≤

2

2

，m≠0．…（15分）

点评：本题考查抛物线方程，考查直线与圆的位置关系，考查学生分析解决问题的能力，属于中档题．