题目内容
已知等差数列{an}的前n项和为Sn,且a2=5,S5=55.
(Ⅰ)求an及Sn;
(Ⅱ)若数列{
}的前n项和Tn,试求Tn并证明不等式
≤Tn<1成立.
(Ⅰ)求an及Sn;
(Ⅱ)若数列{
| 4 |
| an2-1 |
| 1 |
| 2 |
考点:数列与不等式的综合,等差数列的前n项和,数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)设等差数列{an}的首项为a1,公差为d,利用a2=5,S5=55求出首项与公差,即可求解an及Sn;
(Ⅱ)化简
,利用裂项法求出前n项和Tn,通过判断前n项和Tn的单调性,求出最小值即可证明结果.
(Ⅱ)化简
| 4 |
| an2-1 |
解答:
解:(Ⅰ)设等差数列{an}的首项为a1,公差为d,
∵a2=5,S9=99,∴99=
=9a5,得a5=11
∴3d=a5-a2=6,∴d=2,a1=3-------------------------------------(4分)
∴an=2n+1-------------------------------------(6分)
(Ⅱ)bn=
=
=
=
-
------------------------------(9分)
∴Tn=b1+b2+…+bn=(1-
)+(
-
)+…+(
-
)=1-
<1------------(11分)
又因为Tn+1-Tn=
>0,所以Tn>Tn-1>…>T1=
所以
≤Tn<1------------------------------------------------(12分)
∵a2=5,S9=99,∴99=
| 9×(a1+a9) |
| 2 |
∴3d=a5-a2=6,∴d=2,a1=3-------------------------------------(4分)
∴an=2n+1-------------------------------------(6分)
(Ⅱ)bn=
| 4 | ||
|
| 4 |
| 4n(n+1) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=b1+b2+…+bn=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
又因为Tn+1-Tn=
| 1 |
| (n+1)(n+2) |
| 1 |
| 2 |
所以
| 1 |
| 2 |
点评:本题考查数列求和,等差数列的应用,数列的函数的特征,数列与不等式的关系,是中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
下列函数是偶函数且在区间(-∞,0)上为增函数的是( )
A、y=x
| ||
| B、y=x2-1 | ||
| C、y=|x| | ||
| D、y=2-|x| |
若函数y=ax-(b+1)(a>0,a≠1)的图象在第一、三、四象限,则有( )
| A、a>1且b<1 |
| B、a>1且b>0 |
| C、0<a<1且b>0 |
| D、0<a<1且b<0 |
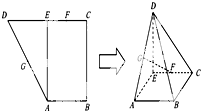 如图,已知直角梯形ABCD中,E为CD边中点,且AE⊥CD,又G,F分别为DA,EC的中点,将△ADE沿AE折叠,使得DE⊥EC.
如图,已知直角梯形ABCD中,E为CD边中点,且AE⊥CD,又G,F分别为DA,EC的中点,将△ADE沿AE折叠,使得DE⊥EC.