题目内容
若函数y=ax-(b+1)(a>0,a≠1)的图象在第一、三、四象限,则有( )
| A、a>1且b<1 |
| B、a>1且b>0 |
| C、0<a<1且b>0 |
| D、0<a<1且b<0 |
考点:指数函数的单调性与特殊点
专题:函数的性质及应用
分析:根据图象的性质可得:a>1,a0-b-1<0,即可求解.
解答:
解:∵函数y=ax-(b+1)(a>0,a≠1)的图象在第一、三、四象限,
∴根据图象的性质可得:a>1,a0-b-1<0,
即a>1,b>0,
故选:B
∴根据图象的性质可得:a>1,a0-b-1<0,
即a>1,b>0,
故选:B
点评:本题考查了指数函数的性质,图象的运用,属于中档题,对图象要求较高.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
以圆x2+2x+y2=0的圆心为圆心,半径为2的圆的方程是( )
| A、(x-1)2+y2=4 |
| B、(x-1)2+y2=2 |
| C、(x+1)2+y2=2 |
| D、(x+1)2+y2=4 |
函数y=-x2-4x+1,x∈[-4,1],的最小值为( )
| A、5 | B、-4 | C、-5 | D、1 |
已知函数f(x)=cos
cos(
+2x),则函数f(x)满足( )
| 2π |
| 3 |
| π |
| 2 |
| A、f(x)的最小正周期是2π | ||||||||||||
| B、若f(x1)=f(x2),则x1=x2 | ||||||||||||
C、f(x)的图象关于直线x=
| ||||||||||||
D、当x∈[-
|
经过抛物线x2=4y的焦点和双曲线
-
=1的右焦点的直线方程为( )
| x2 |
| 4 |
| y2 |
| 5 |
| A、3x+y-3=0 |
| B、x+3y-3=0 |
| C、x+48y-3=0 |
| D、48x+y-3=0 |
如图,在地面A处测得树梢的仰角为60°,A与树底部B相距为5米,则树高度( )
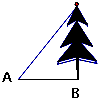

A、5
| ||||
| B、5米 | ||||
| C、10米 | ||||
D、
|
如果命题“p∨q”为真命题,则( )
| A、p,q中至少有一个为真命题 |
| B、p,q均为假命题 |
| C、p,q均为真命题 |
| D、p,q中至多有一个为真命题 |
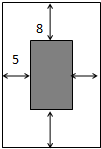 如图设计一幅矩形宣传画,要求画面(阴影部分)面积为4840cm2,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
如图设计一幅矩形宣传画,要求画面(阴影部分)面积为4840cm2,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?