题目内容
设函数f(x)=log2x.
(1)解不等式f(x-1)+f(x)>1;
(2)设函数g(x)=f(2x+1)+kx,若函数g(x)为偶函数,求实数k的值;
(3)当x∈[t+2,t+3]时,是否存在实数t(其中0<t<1),使得不等式|f(
)-f(x-3t)|≤1恒成立?若存在,求出t的取值范围;若不存在,说明理由.
(1)解不等式f(x-1)+f(x)>1;
(2)设函数g(x)=f(2x+1)+kx,若函数g(x)为偶函数,求实数k的值;
(3)当x∈[t+2,t+3]时,是否存在实数t(其中0<t<1),使得不等式|f(
| 1 |
| x-t |
考点:函数恒成立问题,函数奇偶性的判断,对数的运算性质,指、对数不等式的解法
专题:函数的性质及应用
分析:(1)化简f(x-1)+f(x)>1;利用对数不等式转化为不等式组,求解即可.
(2)通过函数g(x)为偶函数,利用偶函数的定义推出方程,即可求实数k的值;
(3)转化不等式|f(
)-f(x-3t)|≤1恒成立,为函数的最值问题,通过绝对值函数的最值,求出t的取值范围即可.
(2)通过函数g(x)为偶函数,利用偶函数的定义推出方程,即可求实数k的值;
(3)转化不等式|f(
| 1 |
| x-t |
解答:
(本题满分16分)本题共有3个小题,第1小题满分(4分),第2小题满分(5分),第3小题满分(7分).
解(1)log2x+log2(x-1)>2,可得:
,
解得x>2(4分)(给出x<-1或x>2扣1分)
(2)g(-x)=g(x),即log2(2-x+1)-kx=log2(2x+1)+kx,(5分)
整理,得(2k+1)x=0,k=-
; (9分)
(如g(-1)=g(1),k=-
,没有证明扣2分)
(3)不等式|f(
)-f(x-3t)|≤1恒成立,
即|log2
-log2(x-3t)|=|log2(x-t)(x-3t)|≤1,(11分)
等价于
≤h(x)=(x-t)(x-3t)≤2恒成立,
解h(x)max=h(t+3)≤2,h(x)min=h(t+2)≥
,得t≤
,t≥
,
综上,不存在t符合题意. (16分)
解(1)log2x+log2(x-1)>2,可得:
|
解得x>2(4分)(给出x<-1或x>2扣1分)
(2)g(-x)=g(x),即log2(2-x+1)-kx=log2(2x+1)+kx,(5分)
整理,得(2k+1)x=0,k=-
| 1 |
| 2 |
(如g(-1)=g(1),k=-
| 1 |
| 2 |
(3)不等式|f(
| 1 |
| x-t |
即|log2
| 1 |
| x-t |
等价于
| 1 |
| 2 |
解h(x)max=h(t+3)≤2,h(x)min=h(t+2)≥
| 1 |
| 2 |
| 7 |
| 8 |
| 7 |
| 6 |
综上,不存在t符合题意. (16分)
点评:本题考查对数不等式的解法,函数的最值,转化思想的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
经过抛物线x2=4y的焦点和双曲线
-
=1的右焦点的直线方程为( )
| x2 |
| 4 |
| y2 |
| 5 |
| A、3x+y-3=0 |
| B、x+3y-3=0 |
| C、x+48y-3=0 |
| D、48x+y-3=0 |
如图,在地面A处测得树梢的仰角为60°,A与树底部B相距为5米,则树高度( )
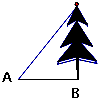

A、5
| ||||
| B、5米 | ||||
| C、10米 | ||||
D、
|
| ||||||||
(
|
| A、1 | ||
B、m
| ||
C、m
| ||
| D、m |
如果命题“p∨q”为真命题,则( )
| A、p,q中至少有一个为真命题 |
| B、p,q均为假命题 |
| C、p,q均为真命题 |
| D、p,q中至多有一个为真命题 |
设a=log
0.6,b=log20.6,c=20.6,则a,b,c的大小关系是( )
| 1 |
| 2 |
| A、a<b<c |
| B、b<c<a |
| C、b<a<c |
| D、c<a<b |