题目内容
9.设$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$是两个不共线的向量,已知$\overrightarrow{AB}$=2$\overrightarrow{{e}_{1}}$+k$\overrightarrow{{e}_{2}}$,$\overrightarrow{BC}$=$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$,$\overrightarrow{CD}$=2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,若A、B、D三点共线,求k的值为$\frac{4}{3}$.分析 利用向量共线定理即可得出.
解答 解:$\overrightarrow{BD}$=$\overrightarrow{BC}+\overrightarrow{CD}$=$3\overrightarrow{{e}_{1}}+2\overrightarrow{{e}_{2}}$,
∵A、B、D三点共线,
∴存在实数m使得$\overrightarrow{AB}$=m$\overrightarrow{BD}$,
∴2$\overrightarrow{{e}_{1}}$+k$\overrightarrow{{e}_{2}}$=m($3\overrightarrow{{e}_{1}}+2\overrightarrow{{e}_{2}}$),∴2=3m,k=2m,
解得k=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查了平面向量共线定理,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
1.中心角为60°的扇形AOB,它的弧长为2π,则三角形AOB的内切圆半径为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
4.函数f(x)=-4x3+3x+2(x∈[0,1])的最大值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.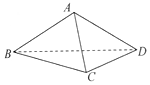 如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,直线AC与底面BCD所成角的大小为( )
如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,直线AC与底面BCD所成角的大小为( )
 如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,直线AC与底面BCD所成角的大小为( )
如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,直线AC与底面BCD所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
1.已知动点M(x,y)的坐标满足方程$\sqrt{{{(y+5)}^2}+{x^2}}-\sqrt{{{(y-5)}^2}+{x^2}}=8$,则M的轨迹方程是( )
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{9}=1(x>0)$ | D. | $\frac{y^2}{16}-\frac{x^2}{9}=1(y>0)$ |
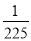 B.
B.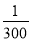 C.
C.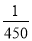 D.以上全不对
D.以上全不对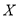 表示2台机器三年内共需更换的易损零件数,
表示2台机器三年内共需更换的易损零件数,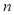 表示购买2台机器的同时购买的易损零件数.
表示购买2台机器的同时购买的易损零件数.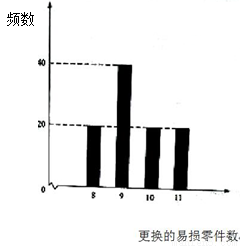
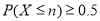 ,确定
,确定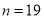 与
与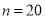 之中选其一,应选用哪个?
之中选其一,应选用哪个?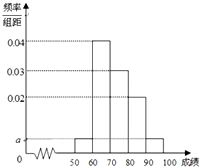 某校100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].