题目内容
1.已知含有n个元素的正整数集A={a1,a2,…,an}(a1<a2<…<an,n≥3)具有性质P:对任意不大于S(A)(其中S(A)=a1+a2+…+an)的正整数k,存在数集A的一个子集,使得该子集所有元素的和等于k.(Ⅰ)写出a1,a2的值;
(Ⅱ)证明:“a1,a2,…,an成等差数列”的充要条件是“S(A)=$\frac{n(n+1)}{2}$”;
(Ⅲ)若S(A)=2017,求当n取最小值时an的最大值.
分析 (Ⅰ)由由an为正整数,则a1=1,a2=2.a1<a2<…<an,n≥3,即可求得a1=1,a2=2;
(Ⅱ)先证明充分性,由a1,a2,…,an成等差数列,则an=n,由等差数列通项公式即可求得S(A)=$\frac{n(n+1)}{2}$”;再证明必要性,由$S(A)={a_1}+{a_2}+…+{a_n}≥1+2+…+n=\frac{n(n+1)}{2}$,则am=m(m=1,2,…,n),故a1,a2,…,an为等差数列;
(Ⅲ)由题意可知:$?{a_m}≤{2^{m-1}}$(m=1,2,…,n).因此$2017={a_1}+{a_2}+…+{a_n}≤1+2+…+{2^{n-1}}={2^n}-1$,即2n≥2018,所以n≥11.分类,由集合的性质,分类,即可求得当n取最小值11时,an的最大值为1009.
解答 解:(Ⅰ)由集合A={a1,a2,…,an},}(a1<a2<…<an,n≥3),
由an为正整数,则a1=1,a2=2.
(Ⅱ)先证必要性:
因为a1=1,a2=2,又a1,a2,…,an成等差数列,故an=n,所以$S(A)=\frac{n(n+1)}{2}$;
再证充分性:
因为a1<a2<…<an,a1,a2,…,an为正整数数列,故有a1=1,a2=2,a3≥3,a4≥4,…,an≥n,
所以$S(A)={a_1}+{a_2}+…+{a_n}≥1+2+…+n=\frac{n(n+1)}{2}$,
又$S(A)=\frac{n(n+1)}{2}$,故am=m(m=1,2,…,n),故a1,a2,…,an为等差数列.
(Ⅲ)先证明$?{a_m}≤{2^{m-1}}$(m=1,2,…,n).
假设存在${a_p}>{2^{p-1}}$,且p为最小的正整数.
依题意p≥3,则a1+a2+…+ap-1≤1+2+…+2p-2=2p-1-1,又因为a1<a2<…<an,
故当k∈(2p-1-1,ap)时,k不能等于集合A的任何一个子集所有元素的和.
故假设不成立,即$?{a_m}≤{2^{m-1}}$(m=1,2,…,n)成立.
因此$2017={a_1}+{a_2}+…+{a_n}≤1+2+…+{2^{n-1}}={2^n}-1$,
即2n≥2018,所以n≥11.
因为S=2017,则a1+a2+…+an-1=2017-an,
若2017-an<an-1时,则当k∈(2017-an,an)时,集合A中不可能存在若干不同元素的和为k,
故2017-an≥an-1,即an≤1009.
此时可构造集合A={1,2,4,8,16,32,64,128,256,497,1009}.
因为当k∈{2,2+1}时,k可以等于集合{1,2}中若干个元素的和;
故当k∈{22,22+1,22+2,22+3}时,k可以等于集合{1,2,22}中若干不同元素的和;
…
故当k∈{28,28+1,28+2,…,28+255}时,k可以等于集合{1,2,…,28}中若干不同元素的和;
故当k∈{497+3,497+4,…,497+511}时,k可以等于集合{1,2,…,28,497}中若干不同元素的和;
故当k∈{1009,1009+1,1009+2,…,1009+1008}时,k可以等于集合{1,2,…,28,497,1009}中若干不同元素的和,
所以集合A={1,2,4,8,16,32,64,128,256,497,1009}满足题设,
所以当n取最小值11时,an的最大值为1009.
点评 本题考查数列的求和,等差数列的性质,突出考查反证法的应用,考查分类讨论思想与转化思想,考查构造函数的思想,属于难题.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案| A. | 图象M关于直线x=-$\frac{π}{12}$对称 | |
| B. | 由y=2sin2x的图象向左平移$\frac{π}{6}$得到M | |
| C. | 图象M关于点(-$\frac{π}{12}$,0)对称 | |
| D. | f(x)在区间(-$\frac{π}{12}$,$\frac{5π}{12}$)上递增 |
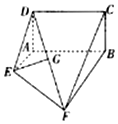 已知多面体ABCDEF如图所示,其中ABCD为矩形,△DAE为等腰等腰三角形,DA⊥AE,四边形AEFB为梯形,且AE∥BF,∠ABF=90°,AB=BF=2AE=2.
已知多面体ABCDEF如图所示,其中ABCD为矩形,△DAE为等腰等腰三角形,DA⊥AE,四边形AEFB为梯形,且AE∥BF,∠ABF=90°,AB=BF=2AE=2.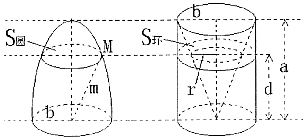 祖暅(公元前5-6世纪),祖冲之之子,是我国齐梁时代的数学家.他提出了一条原理:“幂势既同,則积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面,可以证明S圆=S环知总成立.据此,短轴长为4cm,长轴为6cm的椭球体的体积是16πcm3.
祖暅(公元前5-6世纪),祖冲之之子,是我国齐梁时代的数学家.他提出了一条原理:“幂势既同,則积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面,可以证明S圆=S环知总成立.据此,短轴长为4cm,长轴为6cm的椭球体的体积是16πcm3.