题目内容
4.函数f(x)=-4x3+3x+2(x∈[0,1])的最大值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 求出原函数的导函数,由导函数为0得到导函数的零点,由导函数的零点对区间(0,1)分段,利用导函数在各区间段内的符号可得原函数的单调性,从而求得函数在闭区间上的最值.
解答 解:由f(x)=-4x3+3x+2,得f′(x)=-12x2+3,
由f′(x)=-12x2+3=0,得x=$±\frac{1}{2}$.
∴当x∈(0,$\frac{1}{2}$)时,f′(x)>0,当x∈($\frac{1}{2}$,+∞)时,f′(x)<0,
f(x)在(0,$\frac{1}{2}$)上为增函数,在($\frac{1}{2}$,+∞)上为减函数.
∴f(x)的最大值为f($\frac{1}{2}$)=$-4×(\frac{1}{2})^{3}+3×\frac{1}{2}+2=3$.
故选:C.
点评 本题考查利用导数研究函数在闭区间上的最值,考查导函数的符号与原函数单调性间的关系,是中档题.

练习册系列答案
相关题目
13.一个三位自然数百位,十位,个位上的数字依次为a,b,c,当且仅当a>b,b<c时称为“凹数”(如213),若a,b,c∈{1,2,3,4},且a,b,c互不相同,则这个三位数为“凹数”的有( )个.
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
16.半径为3cm的圆中,$\frac{π}{7}$的圆心角所对的弧长为( )
| A. | $\frac{3π}{7}$cm | B. | $\frac{π}{21}$cm | C. | $\frac{3}{7}$cm | D. | $\frac{9π}{7}$cm |
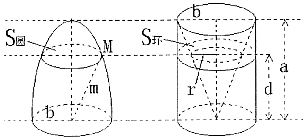 祖暅(公元前5-6世纪),祖冲之之子,是我国齐梁时代的数学家.他提出了一条原理:“幂势既同,則积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面,可以证明S圆=S环知总成立.据此,短轴长为4cm,长轴为6cm的椭球体的体积是16πcm3.
祖暅(公元前5-6世纪),祖冲之之子,是我国齐梁时代的数学家.他提出了一条原理:“幂势既同,則积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面,可以证明S圆=S环知总成立.据此,短轴长为4cm,长轴为6cm的椭球体的体积是16πcm3. ,2),倾斜角为60°的直线方程是( )
,2),倾斜角为60°的直线方程是( )



 、
、 , 平面α,
, 平面α,  ∥
∥ ,
,  ∥α, 那么
∥α, 那么 与平面α的关系是( ).
与平面α的关系是( ). ∥α
∥α
 α
α ∥α或
∥α或
 α
α 与α相交
与α相交