题目内容
14．
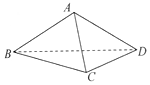如图，在三棱锥A-BCD中，侧面ABD⊥底面BCD，BC⊥CD，AB=AD=4，BC=6，BD=4$\sqrt{3}$，直线AC与底面BCD所成角的大小为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
分析 面ABD⊥底面BCD，AB=AD，取DB中点O，则AO⊥面BCD，即∠ACO就是直线AC与底面BCD所成角，解三角形即可求得角的大小．
解答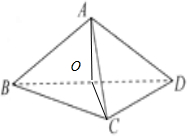 
解：∵面ABD⊥底面BCD，AB=AD，取DB中点O，则AO⊥面BCD，
∴∠ACO就是直线AC与底面BCD所成角．
∵BC⊥CD，BC=6，BD=4$\sqrt{3}$，∴CO=2$\sqrt{3}$，
在Rt△ADO中，OD=$\sqrt{A{D}^{2}-O{D}^{2}}=2$，
在Rt△AOC中，tan∠ACO=$\frac{AO}{OC}=\frac{\sqrt{3}}{3}$．
直线AC与底面BCD所成角的大小为300．
故选：A．
点评 本题考查了直线与平面所成角的求解，找到所求的角是关键，属于中档题．
练习册系列答案
相关题目
6．函数f（x）=2sin（2x+$\frac{π}{6}$）的图象为M，则下列结论中正确的是（ ）
| A． | 图象M关于直线x=-$\frac{π}{12}$对称 | |
| B． | 由y=2sin2x的图象向左平移$\frac{π}{6}$得到M | |
| C． | 图象M关于点（-$\frac{π}{12}$，0）对称 | |
| D． | f（x）在区间（-$\frac{π}{12}$，$\frac{5π}{12}$）上递增 |
2．已知函数$f（x）=\left\{\begin{array}{l}|{{{log}_4}x}|，\;0＜x≤4\\{x^2}-10x+25，\;x＞4.\end{array}\right.$若a，b，c，d是互不相同的正数，且f（a）=f（b）=f（c）=f（d），则abcd的取值范围是（ ）
| A． | （24，25） | B． | （18，24） | C． | （21，24） | D． | （18，25） |
5．函数$y=sin（2x+\frac{π}{3}）$的图象（ ）
| A． | 关于点$[{\frac{π}{3}，0}]$对称 | B． | 关于直线$x=\frac{π}{4}$对称 | ||
| C． | 关于点$[{\frac{π}{4}，0}]$对称 | D． | 关于直线$x=\frac{π}{3}$对称 |
，对于任意
，都存在
，使得
，则
的最小值为________.