题目内容
19.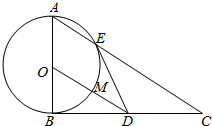 如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.
如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.(1)若∠EDO=30°,求∠AOD;
(2)求证:DE•BC=DM•AC+DM•AB.
分析 (1)连接BE,OE,由已知得∠ABC=90°=∠AEB,∠A=∠A,从而△AEB∽△ABC,进而∠ABE=∠C,进而∠BEO+∠DEB=∠DCE+∠CBE=90°,由此能证明DE是圆O的切线,利用∠EDO=30°,求∠AOD;
(2)DM=OD-OM=$\frac{1}{2}$(AC-AB),从而DM•AC+DM•AB=$\frac{1}{2}$(AC-AB)•(AC+AB)=$\frac{1}{2}$BC2,由此能证明DE•BC=DM•AC+DM•AB.
解答  (1)解:连接BE,OE.
(1)解:连接BE,OE.
∵AB是直径,∴∠AEB=90°,
∵∠ABC=90°=∠AEB,∠A=∠A,∴△AEB∽△ABC,
∴∠ABE=∠C,
∵BE⊥AC,D为BC的中点,∴DE=BD=DC,
∴∠DEC=∠DCE=∠ABE=∠BEO,∠DBE=∠DEB,
∴∠BEO+∠DEB=∠DCE+∠CBE=90°,
∴∠OED=90°,∴DE是圆O的切线.
∵∠EDO=30°,
∴∠DBE=∠DEB=∠A=60°,
∴∠AOD=120°;
(2)证明:∵O、D分别为AB、BC的中点,
∴DM=OD-OM=$\frac{1}{2}$(AC-AB),
∴DM•AC+DM•AB
=DM•(AC+AB)
=$\frac{1}{2}$(AC-AB)•(AC+AB)
=$\frac{1}{2}$(AC2-AB2)
=$\frac{1}{2}$BC2
=DE•BC.
∴DE•BC=DM•AC+DM•AB.
点评 本题考查DE•BC=DM•AC+DM•AB的证明,考查学生分析解决问题的能力,是中档题,解题时要认真审题,注意弦切角定理的合理运用.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
10.设函数f(x)是定义在R上的偶函数,且对任意的x∈R,都有f(x+2)=f(x).当-1≤x≤0时,f(x)=-x2,若直线y=-x+m与函数y=f(x)的图象有两个不同的公共点,则实数m的值为( )
| A. | 2k-$\frac{1}{4}$(k∈Z) | B. | 2k+$\frac{1}{4}$(k∈Z) | C. | 2k或2k-$\frac{1}{4}$(k∈Z) | D. | 2k或2k+$\frac{1}{4}$(k∈Z) |
7.2015年高中生技能大赛中三所学校分别有3名、2名、1名学生获奖,这6名学生要排成一排合影,则同校学生排在一起的概率是( )
| A. | $\frac{1}{30}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{5}$ |
4.已知表面积为24π的球体,其内接正四棱柱(底面是正方形,侧棱垂直于底面)的高为4,则这个正四棱柱的侧面积为( )
| A. | 32 | B. | 36 | C. | 48 | D. | 64 |
11.已知某几何体的三视图如图所示,则该几何体的表面积( )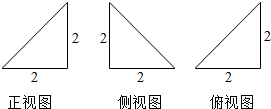

| A. | 6 | B. | $6+2\sqrt{3}$ | C. | $8+8\sqrt{2}$ | D. | $4+4\sqrt{2}$ |
9. 每年七夕,琳琅满目的饰品在各大品牌店中成为年轻人亲眯的对象,这也使各大珠宝公司挖空心思,设计出匠心独运的饰品.某珠宝公司市场专员甲对该公司的一款项链的单价x(百元)和单位时间内的销售量y(件)之间的关系作出价格分析,所得数据如下:
每年七夕,琳琅满目的饰品在各大品牌店中成为年轻人亲眯的对象,这也使各大珠宝公司挖空心思,设计出匠心独运的饰品.某珠宝公司市场专员甲对该公司的一款项链的单价x(百元)和单位时间内的销售量y(件)之间的关系作出价格分析,所得数据如下:
其中价格x(元)恰为公差为2的等差数列{an}的前5项,且等差数列{an}的前10项和为230.
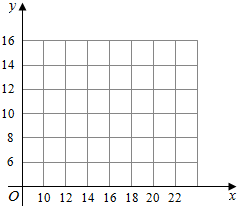
(1)请根据上述数据在下列网格纸中绘制散点图;
(2)请根据表格数据计算项链的单价x(百元)和单位时间内的销售量y(件)之间的回归直线方程.
$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}}\\{\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$.
 每年七夕,琳琅满目的饰品在各大品牌店中成为年轻人亲眯的对象,这也使各大珠宝公司挖空心思,设计出匠心独运的饰品.某珠宝公司市场专员甲对该公司的一款项链的单价x(百元)和单位时间内的销售量y(件)之间的关系作出价格分析,所得数据如下:
每年七夕,琳琅满目的饰品在各大品牌店中成为年轻人亲眯的对象,这也使各大珠宝公司挖空心思,设计出匠心独运的饰品.某珠宝公司市场专员甲对该公司的一款项链的单价x(百元)和单位时间内的销售量y(件)之间的关系作出价格分析,所得数据如下:| 单价x(百元) | a1 | a2 | a3 | a4 | a5 |
| 单位时间内销售量y(件) | 14 | 13 | 10 | 7 | 5 |
(1)请根据上述数据在下列网格纸中绘制散点图;
(2)请根据表格数据计算项链的单价x(百元)和单位时间内的销售量y(件)之间的回归直线方程.
$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}}\\{\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$.
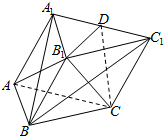 如图,已知三棱柱ABC-A1B1C1的侧面BCC1B1是菱形,D为A1C1的中点,B1C⊥A1B.
如图,已知三棱柱ABC-A1B1C1的侧面BCC1B1是菱形,D为A1C1的中点,B1C⊥A1B.