题目内容
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了4次试验.收集数据如下:
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
=
x+
;
(Ⅲ)现需生产20件此零件,预测需用多长时间?
(注:用最小二乘法求线性回归方程系数公式
=
,
=
-
)
| 零件个数x(个) | 1 | 2 | 3 | 4 |
| 加工时间y(小时) | 2 | 3 | 5 | 8 |
(Ⅱ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 |
| y |
 |
| b |
 |
| a |
(Ⅲ)现需生产20件此零件,预测需用多长时间?
(注:用最小二乘法求线性回归方程系数公式
 |
| b |
| |||||||
|
 |
| a |
. |
| y |
 |
| b |
. |
| x |
考点:线性回归方程
专题:阅读型
分析:(I)取值描点可得散点图;
(II)利用最小二乘法求回归直线方程的系数,可得直线方程;
(III)代入当x=20,求得预报变量y值.
(II)利用最小二乘法求回归直线方程的系数,可得直线方程;
(III)代入当x=20,求得预报变量y值.
解答:
解:(I)描点作图:

(II)
=2.5,
=4,
∴
=
=1.4,
=4-1.4×2.5=0.5,
∴回归直线方程为:y=1.4x+0.5;
(III)当x=20时,y=1.4×20+0.5=28.5(小时).

(II)
. |
| x |
. |
| y |
∴
 |
| b |
| 1×2+2×3+3×5+4×6-4×2.5×4 |
| 12+22+32+42-4×2.52 |
 |
| a |
∴回归直线方程为:y=1.4x+0.5;
(III)当x=20时,y=1.4×20+0.5=28.5(小时).
点评:本题考查了线性回归方程的求法及应用,解题的关键是利用最小二乘法求得回归直线方程的系数.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目

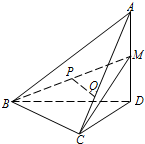 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2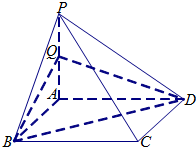 如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.
如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.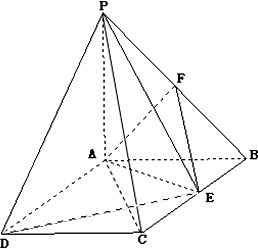 如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,点E,F分别是BC,PB的中点.
如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,点E,F分别是BC,PB的中点.