题目内容
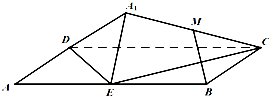如图，矩形ABCD中，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE．若M为线段A1C的中点，则在△ADE翻转过程中，正确的命题是①MB总是平行平面A1DE；
②|BM|是定值；
③点M在圆上运动．
考点：平面与平面之间的位置关系
专题：综合题,空间位置关系与距离
分析：取CD中点F，连接MF，BF，则平面MBF∥平面A1DE，可得①正确；由余弦定理可得MB2=MN2+NB2-2MN•NB•cos∠MNB，所以MB是定值，M是在以B为圆心，MB为半径的圆上，可得②③正确．
解答：
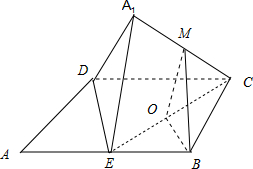解：取CD中点F，连接MF，BF，则MF∥DA1，BF∥DE，∴平面MBF∥平面A1DE，∴MB∥平面A1DE，故①正确
由∠A1DE=∠MNB，MN=
A1D=定值，NB=DE=定值，
由余弦定理可得MB2=MN2+NB2-2MN•NB•cos∠MNB，所以MB是定值，故②正确．
∵B是定点，∴M是在以B为圆心，MB为半径的圆上，故③正确，
故答案为：①②③．
解：取CD中点F，连接MF，BF，则MF∥DA1，BF∥DE，∴平面MBF∥平面A1DE，∴MB∥平面A1DE，故①正确由∠A1DE=∠MNB，MN=
| 1 |
| 2 |
由余弦定理可得MB2=MN2+NB2-2MN•NB•cos∠MNB，所以MB是定值，故②正确．
∵B是定点，∴M是在以B为圆心，MB为半径的圆上，故③正确，
故答案为：①②③．
点评：掌握线面、面面平行与垂直的判定和性质定理及线面角、二面角的定义及求法是解题的关键．
练习册系列答案
应用题作业本系列答案
相关题目
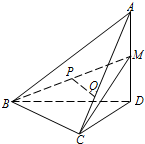如图，在四面体A-BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2