题目内容
某货轮匀速行驶在相距300海里的甲、乙两地间，运输成本由燃料费用和其它费用组成，已知该货轮每小时的燃料费用与其航行速度的平方成正比（比例系数为0.5），其它费用为每小时m元，根据市场调研，得知m的波动区间是[1000，1600]，且该货轮的最大航行速度为50海里/小时．
（1）请将从甲地到乙地的运输成本y（元）表示为航行速度x（海里/小时）的函数；
（2）要使从甲地到乙地的运输成本最少，该货轮应以多大的航行速度行驶？
（1）请将从甲地到乙地的运输成本y（元）表示为航行速度x（海里/小时）的函数；
（2）要使从甲地到乙地的运输成本最少，该货轮应以多大的航行速度行驶？
考点：解三角形的实际应用
专题：不等式的解法及应用
分析：（1）从甲地到乙地的运输成本y（元）=每小时的燃料费用×时间+每小时其它费用×时间；
（2）由（Ⅰ）求得函数表达式，用基本不等式可求得最小值．
（2）由（Ⅰ）求得函数表达式，用基本不等式可求得最小值．
解答：
解：（1）由题意，每小时的燃料费用为：0.5x2（0＜x≤50），从甲地到乙地所用的时间为
小时，
则从甲地到乙地的运输成本y=0.5x2•
+
•m，（0＜x≤50），
故所求函数y=150（x+
），（0＜x≤50），
（2）由（Ⅰ）知，y=150（x+
）≥150•2
=300
，当且仅当x=
时，即x=
时，运输成本最少．
答：要使从甲地到乙地的运输成本最少，该货轮应以每小时
海里的速度行驶．
| 300 |
| x |
则从甲地到乙地的运输成本y=0.5x2•
| 300 |
| x |
| 300 |
| x |
故所求函数y=150（x+
| 2m |
| x |
（2）由（Ⅰ）知，y=150（x+
| 2m |
| x |
x•
|
| 2m |
| 2m |
| x |
| 2m |
答：要使从甲地到乙地的运输成本最少，该货轮应以每小时
| 2m |
点评：本题考查了由函数模型建立目标函数，利用基本不等式求函数最值的问题，属于中档题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
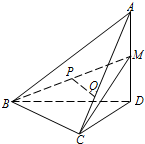如图，在四面体A-BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2
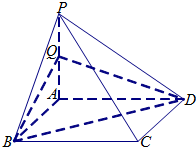如图所示，四棱锥P-ABCD中，底面ABCD是边长为2的正方形，侧棱PA⊥底面ABCD，且PA=2，Q是PA的中点．