题目内容
设函数f(x)=2sin(2ωx-
)+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
,1)
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点(
,0),求函数f(x)的值域.
| π |
| 6 |
| 1 |
| 2 |
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点(
| π |
| 4 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)令 2x-
=kπ+
,k∈z,可得函数的图象关于直线x=
+
,k∈z对称.再根据函数的图象关于直线x=π对称,且ω∈(
,1),可得ω的值,可得函数的最小正周期
(2)把点(
,0)代入函数的解析式求得λ=0,可得f(x)的解析式,从而求得函数f(x)的值域.
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2ω |
| π |
| 3ω |
| 1 |
| 2 |
(2)把点(
| π |
| 4 |
解答:
解:(1)令 2x-
=kπ+
,k∈z,可得x=
+
,k∈z,故函数的图象关于直线x=
+
,k∈z对称.
再根据函数的图象关于直线x=π对称,且ω∈(
,1),可得ω=
.
故函数的最小正周期为
=
.
(2)若y=f(x)的图象经过点(
,0),可得2sin(2×
×
-
)+λ=0,求得λ=-
,
∴f(x)=2sin(
x-
)-
,故函数f(x)的值域为[-2-
,2-
].
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2ω |
| π |
| 3ω |
| kπ |
| 2ω |
| π |
| 3ω |
再根据函数的图象关于直线x=π对称,且ω∈(
| 1 |
| 2 |
| 5 |
| 6 |
故函数的最小正周期为
| 2π | ||
|
| 12π |
| 5 |
(2)若y=f(x)的图象经过点(
| π |
| 4 |
| 5 |
| 6 |
| π |
| 4 |
| π |
| 6 |
| 2 |
∴f(x)=2sin(
| 5 |
| 3 |
| π |
| 6 |
| 2 |
| 2 |
| 2 |
点评:本题主要考查正弦函数的对称性、周期性、值域,属于基础题.

练习册系列答案
相关题目
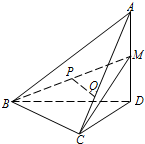 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2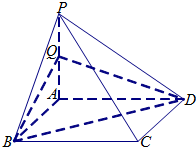 如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.
如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.