题目内容
若复数z满足（l+2i）z=|3+4i|（i为虚数单位），则复数z等于 ．
考点：复数代数形式的混合运算
专题：数系的扩充和复数
分析：利用复数的运算法则和模的计算公式即可得出．
解答：
解：∵复数z满足（l+2i）z=|3+4i|，
∴（1-2i）（1+2i）z=
(1-2i)，
化为5z=5（1-2i），
∴z=1-2i．
故答案为：1-2i．
∴（1-2i）（1+2i）z=
| 32+42 |
化为5z=5（1-2i），
∴z=1-2i．
故答案为：1-2i．
点评：本题考查了复数的运算法则和模的计算公式，属于基础题．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
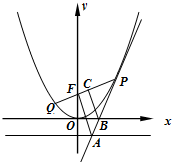已知抛物线C：x2=4y的焦点为F，P是抛物线上异于原点的任意一点，直线PF与抛物线另一交点为点Q，设l是过点P的抛物线的切线，l与直线y=-1和x轴的交点分别为A，B．复数z=1+i，则
+
对应的点所在的象限为（ ）
| 1 |
| z |
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在△ABC中，点M是BC中点．若∠A=120°，
•
=-
，则|
|的最小值是（ ）
| AB |
| AC |
| 1 |
| 2 |
| AM |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|