Question

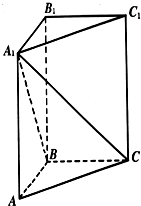在直三棱柱ABC-A₁B₁C₁中，∠ABC=90°，AB=BC=1．
（Ⅰ） 求异面直线B₁C₁与AC所成角的大小；
（Ⅱ） 若该直三棱柱ABC-A₁B₁C₁的体积为

2

2

，求点A到平面A₁BC的距离．

Answer 1

考点：异面直线及其所成的角

专题：直线与圆

分析：（Ⅰ）由BC∥B₁C₁，知∠ACB为异面直线B₁C₁与AC所成角（或它的补角），由此能求出异面直线B₁C₁与AC所成角．
（Ⅱ）设点A到平面A₁BC的距离为h，由三棱锥A₁-ABC的体积=三棱锥A-A₁BC的体积，利用等积法能求出点A到平面A₁BC的距离．

解答： 解：（Ⅰ）∵BC∥B₁C₁，
∴∠ACB为异面直线B₁C₁与AC所成角（或它的补角），（2分）
∵∠ABC=90°，AB=BC=1，∴∠ACB=45°，
∴异面直线B₁C₁与AC所成角为45°．（4分）
（Ⅱ）∵S_△ABC=

1

2

，三棱柱ABC-A₁B₁C₁的体积V=S_△ABC×AA₁₌

2

2

∴AA₁₌

2

，A₁B=

3

（2分）
∵CB⊥平面ABB₁A₁，
∴∠A₁BC=90°，S_△A1BC=

3

2

（4分）
设点A到平面A₁BC的距离为h，
三棱锥A₁-ABC的体积V=

1

3

×S_△ABC×AA₁=三棱锥A-A₁BC的体积V=

1

3

×S_△A1BC×h，
解得h=

6

3

，
∴点A到平面A₁BC的距离为

6

3

．（8分）

点评：本题考查异面直线所成角的求法，考查点到平面的距离的求法，解题时要认真审题，注意空间思维能力的培养．