题目内容
将下列直角坐标方程和极坐标方程互化
(1)y2=4x;
(2)y2+x2-2x-1=0;
(3)2ρcosθ-ρsinθ=4;
(4)ρ=
.
(1)y2=4x;
(2)y2+x2-2x-1=0;
(3)2ρcosθ-ρsinθ=4;
(4)ρ=
| 1 |
| 2-cosθ |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:由条件利用x=ρcosθ,y=ρsinθ,进行极坐标方程与直角坐标方程的互化.
解答:
解:(1)由y2=4x,可得 ρ2•sin2θ=4ρcosθ,即 ρsin2θ=4cosθ.
(2)由y2+x2-2x-1=0,可得 ρ2-2ρcosθ-1=0.
(3)2ρcosθ-ρsinθ=4,即 2x-y-4=0.
(4)ρ=
,即 2ρ-ρcosθ-1=0,化为直角坐标方程为 2
-x-1=0,
即 4(x2+y2)=x2+2x+1,即 3x2+4y2-2x-1=0.
(2)由y2+x2-2x-1=0,可得 ρ2-2ρcosθ-1=0.
(3)2ρcosθ-ρsinθ=4,即 2x-y-4=0.
(4)ρ=
| 1 |
| 2-cosθ |
| x2+y2 |
即 4(x2+y2)=x2+2x+1,即 3x2+4y2-2x-1=0.
点评:本题主要考查曲线的极坐标方程与直角坐标方程的互化,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组,现要从中抽取10名学生,各组内抽取的编号依次增加10进行系统抽样.
已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组,现要从中抽取10名学生,各组内抽取的编号依次增加10进行系统抽样.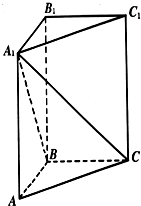 在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1.
在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1.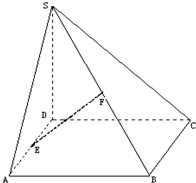 已知:如图,四棱锥S-ABCD底面为平行四边形,E、F分别为边AD、SB中点,
已知:如图,四棱锥S-ABCD底面为平行四边形,E、F分别为边AD、SB中点, 如图为函数y=Asin(ωx+φ)(A,ω>0,|φ|<π)图象的一段.
如图为函数y=Asin(ωx+φ)(A,ω>0,|φ|<π)图象的一段.