题目内容
某学科竞赛的预赛考试分为一试和加试两部分测试,且规定只有一试考试达标着才可以进入加试考试,一试考试和
加试考试都达标才算优胜者,从而进入决赛,一试试卷包括三个独立的必做题目,加试包括两个独立的必做题目,若一试考试至少答对两个问题就认定为达标,加试需两个题目都答对才算达标,假设甲同学一试考试中答对每个题的概率均为
,加试考试中答对每个题的概率都为
,且各题答题情况均互不影响.
(1)求甲同学成为优胜者,顺利进入决赛的概率;
(2)设甲同学解答的题目的个数为X,求X的分布列和期望.
加试考试都达标才算优胜者,从而进入决赛,一试试卷包括三个独立的必做题目,加试包括两个独立的必做题目,若一试考试至少答对两个问题就认定为达标,加试需两个题目都答对才算达标,假设甲同学一试考试中答对每个题的概率均为
| 2 |
| 3 |
| 1 |
| 2 |
(1)求甲同学成为优胜者,顺利进入决赛的概率;
(2)设甲同学解答的题目的个数为X,求X的分布列和期望.
考点:离散型随机变量的期望与方差,互斥事件的概率加法公式,相互独立事件的概率乘法公式,离散型随机变量及其分布列
专题:概率与统计
分析:(1)甲同学成为优胜者,说明甲同学一试和加试均达标,由此能求出甲同学成为优胜者,顺利进入决赛的概率.
(2)X的可能取值为3,5,分别求出相应的概率,由此能求出X的分布列和期望.
(2)X的可能取值为3,5,分别求出相应的概率,由此能求出X的分布列和期望.
解答:
解:(1)甲同学成为优胜者,说明甲同学一试和加试均达标,
则其概率为:
p1=[(
)3+
(
)2×
]×
×
=
.
(2)X的可能取值为3,5,
P(X=3)=(
)3+
(
)2×
=
,
P(X=5)=(
)3+C
(
)2×
=
,
∴X的分布列为:
EX=3×
+5×
=
.
则其概率为:
p1=[(
| 2 |
| 3 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 27 |
(2)X的可能取值为3,5,
P(X=3)=(
| 1 |
| 3 |
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 7 |
| 27 |
P(X=5)=(
| 2 |
| 3 |
2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 20 |
| 27 |
∴X的分布列为:
| X | 3 | 5 | ||||
| P |
|
|
| 7 |
| 27 |
| 20 |
| 27 |
| 121 |
| 27 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
已知点P在直线x+2y-1=0上,点Q在直线x+2y+3=0上,PQ中点为M(x0,y0),且y0≥x0+2,则
的取值范围为( )
| y0 |
| x0 |
A、(-
| ||||
B、[-
| ||||
C、(-
| ||||
D、(-∞,-
|
 已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组,现要从中抽取10名学生,各组内抽取的编号依次增加10进行系统抽样.
已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组,现要从中抽取10名学生,各组内抽取的编号依次增加10进行系统抽样.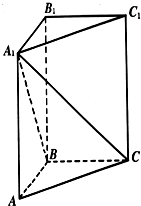 在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1.
在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1.