题目内容

已知在矩阵M对应的变换作用下，点A（1，0）变为A′（1，0），点B（1，1）变为B′（2，1）
（Ⅰ）求矩阵M；
（Ⅱ）求M2，M3，并猜测Mn（只写结果，不必证明）
考点：几种特殊的矩阵变换
专题：选作题,矩阵和变换
分析：（Ⅰ）利用待定系数法，求矩阵M；
（Ⅱ）利用矩阵的乘法求M2，M3，并猜测Mn．
解答： 解：（Ⅰ）设M=
ab
cd
，则
ab
cd
1
0
=
1
0
，
ab
cd
1
1
=
2
1
，

∴
a=1
c=0
a+b=2
c+d=1
，∴a=1，b=1，c=0，d=1，
∴M=
11
01
；
（Ⅱ）M2=
11
01
11
01
=
12
01
，M3=
11
01
11
01
11
01
=
13
01
，猜测Mn=
1n
01
．
点评：本题主要考查矩阵的乘法，考查了二阶矩阵，比较基础．
练习册系列答案
相关题目
设函数f（x）=
3-x-a，x≤0
f(x-1)，x＞0
，若f（x）=x有且仅有三解，则a的取值范围是（　　）
A、[0，2]
B、（-∞，2）
C、（-∞，1]
D、[0，+∞）
已知数列{an}的前n项为和Sn，点（n，
Sn
n
）在直线y=
1
2
x+
11
2
上．数列{bn}满足bn+2-2bn+1+bn=0
（n∈N*），且b3=11，前9项和为153．
（1）求数列{an}，{bn}的通项公式；
（2）设cn=
3
(2an-11)(2bn-1)
，数列{cn}的前n项和为Tn，求使不等式Tn＞
k
57
对一切n∈N*都成立的最大正整数k的值；
（3）设n∈N*，f（n）=
an，n为奇数
bn，n为偶数
，问是否存在m∈N*，使得f（m+15）=5f（m）成立？若存在，求出m的值；若不存在，请说明理由．
（1）已知数列{an}的通项公式为an=（2n+1）•2n-1，用反证法证明数列{an}中任何三项都不可能成等比数列；
（2）用数学归纳法证明不等式n!≤（
n+1
2
）n，n∈N*．
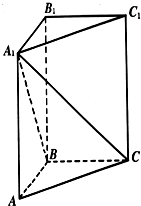在直三棱柱ABC-A1B1C1中，∠ABC=90°，AB=BC=1．
（Ⅰ） 求异面直线B1C1与AC所成角的大小；
（Ⅱ） 若该直三棱柱ABC-A1B1C1的体积为
2
2
，求点A到平面A1BC的距离．
在极坐标系中，已知圆C的圆心坐标为（3，
π
3
），半径为r=3，试写出圆C的极坐标方程．
设函数f（x）=
a
•
b
，其中向量
a
=（2cosx，1），
b
=（cosx，
3
sin2x），x∈R．
（1）求函数y=f（x）的单调区间和对称中心
（2）求函数y=f（x）在[-
π
6
，
π
3
]上的值域．
已知tanα=3x2-1，求α的取值范围．
已知sinα=
5
5
，tanβ=
1
3
，且α、β∈（0，
π
2
）．
（1）求cosα．
（2）求tan（α+β）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网