题目内容
8.已知等差数列{an}前5项和为50,a7=22,数列{bn}的前n项和为Sn,b1=1,bn+1=3Sn+1.(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)若数列{cn}满足$\frac{c_1}{b_1}+\frac{c_2}{b_2}+…+\frac{c_n}{b_n}={a_{n+1}}$,n∈N*,求c1+c2+…+c2017的值.
分析 (I)设等差数列{an}的公差为d,利用等差数列的通项公式及其前n项和公式即可首项和公差,即可求出数列{an}的通项公式,再根据数列的递推公式可得所以{bn}为首项为1,公比为4的等比数列,即可求出数列{bn}的通项公式
(II)根据数列的递推公式先求出{cn}的通项公式,再分组求和.
解答 解:(Ⅰ)设等差数列{an}的公差为d.
依题意得$\left\{\begin{array}{l}5{a_1}+\frac{5×4}{2}d=50\\{a_1}+6d=22\end{array}\right.$,
解得a1=4,d=3,
所以an=a1+(n-1)d=3n+1.
当n=1时,b2=3b1+1=4,
当n≥2时,bn+1=3Sn+1,bn=3Sn-1+1,
以上两式相减得bn+1-bn=3bn,则bn+1=4bn,
又b2=4b1,所以bn+1=4bn,n∈N*.
所以{bn}为首项为1,公比为4的等比数列,
所以${b_n}={4^{n-1}}$.
(Ⅱ)因为$\frac{c_1}{b_1}+\frac{c_2}{b_2}+…+\frac{c_n}{b_n}={a_{n+1}}$,n∈N*
当n≥2时,$\frac{c_1}{b_1}+\frac{c_2}{b_2}+…+\frac{{{c_{n-1}}}}{{{b_{n-1}}}}={a_n}$,
以上两式相减得$\frac{c_n}{b_n}={a_{n+1}}-{a_n}=3$,所以${c_n}=3{b_n}=3×{4^{n-1}}$,n≥2.
当n=1时,$\frac{c_1}{b_1}={a_2}$,所以c1=a2b1=7,不符合上式,
所以c1+c2+…+c2017=7+3(4+42+…+42016)=$7+3×\frac{{4(1-{4^{2016}})}}{1-4}={4^{2017}}+3$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

| A. | 3π | B. | 5π | C. | 10π | D. | 20π |
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
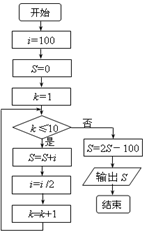 一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )
一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )| A. | 小球第10次着地时向下的运动共经过的路程 | |
| B. | 小球第11次着地时向下的运动共经过的路程 | |
| C. | 小球第10次着地时一共经过的路程 | |
| D. | 小球第11次着地时一共经过的路程 |
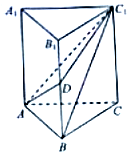 如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为$\frac{1}{3}$.
如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为$\frac{1}{3}$.