��Ŀ����
13��������$\overrightarrow{a}$=��4sin$\frac{��}{2}$x��1����$\overrightarrow{b}$=��$\frac{1}{2}$cos$\frac{��}{2}$x��-1�����أ�0����������f��x��=$\overrightarrow{a}$•$\overrightarrow{b}$+1������[-$\frac{��}{5}$��$\frac{��}{4}$]�ϵ�����������ʵ���ص�ȡֵ��ΧΪ��0��2]������ ����f��x��=sin��x���������Һ����ĵ����Եó�f��x���ĵ��������䣬�Ӷ��г�����ʽ����صķ�Χ��
��� �⣺f��x��=$\overrightarrow{a}•\overrightarrow{b}$+1=2sin$\frac{��}{2}$xcos$\frac{��}{2}$x=sin��x��
��-$\frac{��}{2}$+2k�Сܦ�x��$\frac{��}{2}$+2k�У����-$\frac{��}{2��}$+$\frac{2k��}{��}$��x��$\frac{��}{2��}$+$\frac{2k��}{��}$��k��Z��
�ߦأ�0��
��f��x����һ������������Ϊ[-$\frac{��}{2��}$��$\frac{��}{2��}$]��
��$\left\{\begin{array}{l}{\frac{��}{4}��\frac{��}{2��}}\\{-\frac{��}{5}��-\frac{��}{2��}}\end{array}\right.$�����0���ء�2��
�ʴ�Ϊ��0��2]��
���� ���⿼�������Ǻ����ĺ�ȱ任�����Һ�����ͼ�������ʣ������е��⣮

��ϰ��ϵ�д�
�����Ŀ
3����֪����f��x��=$\left\{\begin{array}{l}|{2^x}-1|��x��1\\|{log_{2017}}��x-1��|��x��1\end{array}$��������f��x��=t���ĸ���ͬ��ʵ����a��b��c��d����a��b��c��d����a+b+$\frac{1}{c}+\frac{1}{d}$��ȡֵ��ΧΪ��������
| A�� | ��-�ޣ�1] | B�� | [1��2017�� | C�� | ��-�ޣ�1�� | D�� | ��1��2017�� |
1����֪����p��?x0��R��ʹtanx0=2��������q��?x��R������x2+2x+1��0��������
| A�� | ����p��q������ | B�� | ����p��q������ | ||
| C�� | ����p�ģ��Vq��Ϊ������ | D�� | ����p�ţ��Vq��Ϊ������ | ||
| E�� | ����p��q������ |
18��һ�������������ͼ����ʾ����ü���������������Ϊ��������
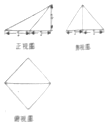

| A�� | 3�� | B�� | 5�� | C�� | 10�� | D�� | 20�� |
2����F1��F2Ϊ˫����$����\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$��a��0��b��0�������ҽ��㣬PΪ����һ�㣬PF2��x�ᴹֱ��ֱ��PF1��б��Ϊ$\frac{3}{4}$����˫���ߦ��Ľ����߷���Ϊ��������
| A�� | y=��x | B�� | $y=��\sqrt{2}x$ | C�� | $y=��\sqrt{3}x$ | D�� | y=��2x |
3����֪��P�����꣨x��y������$\left\{\begin{array}{l}x��-1\\ y��2\\ 2x-y+2��0\end{array}\right.$����P��ֱ��l��ԲO��x2+y2=7����A��B���㣬��|AB|����СֵΪ��������
| A�� | $\sqrt{2}$ | B�� | $2\sqrt{2}$ | C�� | $\sqrt{3}$ | D�� | $2\sqrt{3}$ |