题目内容
8.“2a>2b>1”是“$\root{3}{a}$>$\root{3}{b}$”的( )条件.| A. | 充要 | B. | 必要不充分 | ||
| C. | 充分不必要 | D. | 既不充分也不必要 |
分析 由“2a>2b>1“⇒a>b>0,但是由“$\root{3}{a}$>$\root{3}{b}$“⇒a>b,不一定大于0.即可得出结论.
解答 解:由“2a>2b>1“⇒a>b>0,但是由“$\root{3}{a}$>$\root{3}{b}$“⇒a>b,不一定大于0.
∴“2a>2b>1“是“$\root{3}{a}$>$\root{3}{b}$“的充分不必要条件.
故选:C.
点评 本题考查了函数的单调性、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
3.已知函数f(x)=$\left\{\begin{array}{l}|{2^x}-1|,x≤1\\|{log_{2017}}(x-1)|,x>1\end{array}$,若方程f(x)=t有四个不同的实数根a,b,c,d,且a<b<c<d,则a+b+$\frac{1}{c}+\frac{1}{d}$的取值范围为( )
| A. | (-∞,1] | B. | [1,2017) | C. | (-∞,1) | D. | (1,2017) |
13.已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象过点B(0,-1),且在($\frac{π}{18}$,$\frac{π}{3}$)上单调,同时f(x)的图象向左平移π个单位之后与原来的图象重合,当x1,x2∈(-$\frac{17π}{12}$,-$\frac{2π}{3}$),且x1≠x2时,f(x1)=f(x2),则f(x1+x2)=( )
| A. | -$\sqrt{3}$ | B. | -1 | C. | 1 | D. | $\sqrt{3}$ |
18.一个几何体的三视图如所示,则该几何体的外接球表面积为( )
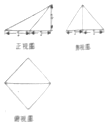

| A. | 3π | B. | 5π | C. | 10π | D. | 20π |
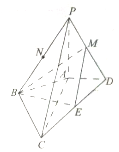 在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N分别为PD,PB,CD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N分别为PD,PB,CD的中点.