��Ŀ����
9��ŷ����ʽeix=cosx+isinx��i��������λ��x��R��������ʿ��������ѧ��ŷ�������ģ�����ָ�������Ķ����������������������Ǻ�����ָ�������Ĺ�ϵ�����ڸ��亯�������м�����Ҫ�ĵ�λ������Ϊ����ѧ�е����š�������ŷ����ʽ����$z={e^{\frac{��}{3}i}}$������z2�ڸ�ƽ��������Ӧ�ĵ�λ�ڣ�������| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
���� �����¶��壬���ɵó��𰸣�
��� �⣺$z={e^{\frac{��}{3}i}}$=cos$\frac{��}{3}$+isin$\frac{��}{3}$=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i��
��z2=��$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i��2=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i��
�˸����ڸ�ƽ���ж�Ӧ�ĵ㣨-$\frac{1}{2}$��$\frac{\sqrt{3}}{2}$��λ��λ�ڵڶ����ޣ�
��ѡ��B��
���� ���⿼���˸�����������ʽ�����Ǻ�����ֵ�������ļ������壬����������������������������ڻ����⣮

��ϰ��ϵ�д�
�����Ŀ
1����֪����p��?x0��R��ʹtanx0=2��������q��?x��R������x2+2x+1��0��������
| A�� | ����p��q������ | B�� | ����p��q������ | ||
| C�� | ����p�ģ��Vq��Ϊ������ | D�� | ����p�ţ��Vq��Ϊ������ | ||
| E�� | ����p��q������ |
18��һ�������������ͼ����ʾ����ü���������������Ϊ��������
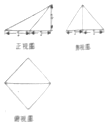

| A�� | 3�� | B�� | 5�� | C�� | 10�� | D�� | 20�� |
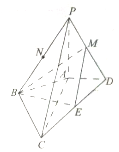 ������P-ABCD�У�PA��ƽ��ABCD��AC��BD��PA=AC=2AD=4��AB=BC=2$\sqrt{5}$��M��N�ֱ�ΪPD��PB��CD���е㣮
������P-ABCD�У�PA��ƽ��ABCD��AC��BD��PA=AC=2AD=4��AB=BC=2$\sqrt{5}$��M��N�ֱ�ΪPD��PB��CD���е㣮 ij���۹�˾Ϊ�˽�Ա�����¹���ˮƽ����1000λԱ���������ȡ100λԱ�����е��飬�õ����µ�Ƶ�ʷֲ�ֱ��ͼ��
ij���۹�˾Ϊ�˽�Ա�����¹���ˮƽ����1000λԱ���������ȡ100λԱ�����е��飬�õ����µ�Ƶ�ʷֲ�ֱ��ͼ��