题目内容
6.已知复数z满足(1+2i)z=i,其中i为虚数单位,则复数z的虚部为$\frac{1}{5}$.分析 利用复数的除法运算化为a+bi(a,b∈R)的形式,则答案可求
解答 解:∵(1+2i)z=i,
∴z=$\frac{i}{1+2i}$=$\frac{i(1-2i)}{5}$=$\frac{2}{5}$+$\frac{i}{5}$,
∴复数z的虚部为$\frac{1}{5}$.
故答案为$\frac{1}{5}$
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知命题p:?x0∈R,使tanx0=2;,命题q:?x∈R,都有x2+2x+1>0,则( )
| A. | 命题p∨q为假命题 | B. | 命题p∧q为真命题 | ||
| C. | 命题p∧(¬q)为真命题 | D. | 命题p∨(¬q)为假命题 | ||
| E. | 命题p∨q为假命题 |
18.一个几何体的三视图如所示,则该几何体的外接球表面积为( )
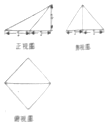

| A. | 3π | B. | 5π | C. | 10π | D. | 20π |
15.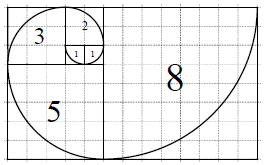 斐波那契数列{an}满足:${a_1}=1,{a_2}=1,{a_n}={a_{n-1}}+{a_{n-2}}({n≥3,n∈{N^*}})$.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n项所占的格子的面积之和为Sn,每段螺旋线与其所在的正方形所围成的扇形面积为cn,则下列结论错误的是( )
斐波那契数列{an}满足:${a_1}=1,{a_2}=1,{a_n}={a_{n-1}}+{a_{n-2}}({n≥3,n∈{N^*}})$.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n项所占的格子的面积之和为Sn,每段螺旋线与其所在的正方形所围成的扇形面积为cn,则下列结论错误的是( )
 斐波那契数列{an}满足:${a_1}=1,{a_2}=1,{a_n}={a_{n-1}}+{a_{n-2}}({n≥3,n∈{N^*}})$.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n项所占的格子的面积之和为Sn,每段螺旋线与其所在的正方形所围成的扇形面积为cn,则下列结论错误的是( )
斐波那契数列{an}满足:${a_1}=1,{a_2}=1,{a_n}={a_{n-1}}+{a_{n-2}}({n≥3,n∈{N^*}})$.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n项所占的格子的面积之和为Sn,每段螺旋线与其所在的正方形所围成的扇形面积为cn,则下列结论错误的是( )| A. | ${S_{n+1}}=a_{n+1}^2+{a_{n+1}}•{a_n}$ | B. | a1+a2+a3+…+an=an+2-1 | ||
| C. | a1+a3+a5+…+a2n-1=a2n-1 | D. | 4(cn-cn-1)=πan-2•an+1 |
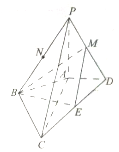 在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N分别为PD,PB,CD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N分别为PD,PB,CD的中点. 某销售公司为了解员工的月工资水平,从1000位员工中随机抽取100位员工进行调查,得到如下的频率分布直方图:
某销售公司为了解员工的月工资水平,从1000位员工中随机抽取100位员工进行调查,得到如下的频率分布直方图: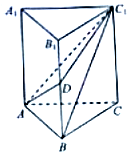 如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为$\frac{1}{3}$.
如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为$\frac{1}{3}$.