题目内容
直线y=2x为双曲线C:
-
=1(a>0,b>0)的一条渐近线,则双曲线C的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:求出双曲线的渐近线方程,可得b=2a,再由a,b,c的关系和离心率公式,计算即可得到.
解答:
解:双曲线C:
-
=1(a>0,b>0)的渐近线方程为y=±
x,
则
=2,即b=2a,
则c=
=
a,
即有e=
=
.
故选:A.
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
则
| b |
| a |
则c=
| a2+b2 |
| 5 |
即有e=
| c |
| a |
| 5 |
故选:A.
点评:本题考查双曲线的方程和性质,考查渐近线方程和离心率的求法,考查运算能力,属于基础题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
已知集合A⊆[0,2π],集合M={y|y=2sin(x+
),x∈A},若M={-1,0,1},则不同集合A的个数是( )
| π |
| 6 |
| A、12 | B、27 | C、42 | D、63 |
双曲线
-
=1(a>0,b>0)的两个焦点为F1,F2,若P为其图象上一点,且|PF1|=3|PF2|,则该双曲线离心率的取值范围为( )
| y2 |
| a2 |
| x2 |
| b2 |
| A、(1,2] |
| B、(1,2) |
| C、(2,+∞) |
| D、[2,+∞) |
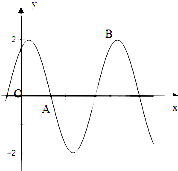 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,图象与x轴交点A及图象最高点B的坐标分别是A(
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,图象与x轴交点A及图象最高点B的坐标分别是A(| π |
| 3 |
| 13π |
| 12 |
| π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
设T=|2x-1|,若不等式T(x)≥(1+
)-|2-
|对任意实数a≠0恒成立,则x的取值范围是( )
| 1 |
| a |
| 1 |
| a |
| A、(-∞,0]∪[1,+∞) |
| B、(0,1] |
| C、(-∞,-1]∪[2,+∞) |
| D、[-1,2] |
△ABC内角A,B,C的对边分别为a,b,c.已知a=3,A=60°,b=
,则B=( )
| 6 |
| A、45° | B、30° |
| C、60° | D、135° |
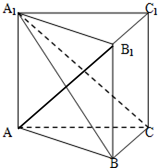 如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面)中,BC⊥AB,且AA1=AB=2.
如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面)中,BC⊥AB,且AA1=AB=2.