Question

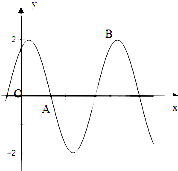函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示，图象与x轴交点A及图象最高点B的坐标分别是A（

π

3

，0），B（

13π

12

，2），则f（-

π

2

）的值为（　　）

• A、-

  3

  2

• B、-

  3

• C、

  3

• D、

  3

  2

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：计算题,三角函数的求值

分析：由图象可得：A=2，

3T

4

=

13π

12

-

π

3

，从而解得ω的值，由B（

13π

12

，2）在函数图象上，|φ|＜π，可解得φ的值，从而求得函数解析式，从而可求f（-

π

2

）的值．

解答： 解：由图象可得：A=2，

3T

4

=

13π

12

-

π

3

，从而解得：T=π．所以ω=

2π

T

=

2π

π

=2．
由因为：B（

13π

12

，2）在函数图象上．
所以可得：2sin（2×

13π

12

+φ）=2，
可解得：2×

13π

12

+φ=2kπ+

3π

2

，k∈Z，即有φ=2kπ-

2π

3

，k∈Z，
∵|φ|＜π，
∴φ=-

2π

3

，
∴f（x）=2sin（2x-

2π

3

），
∴f（-

π

2

）=2sin（-2×

π

2

-

2π

3

）=

3

，
故选：C．

点评：本题主要考查了由y=Asin（ωx+φ）的部分图象确定其解析式，属于基础题．