题目内容
已知函数f(x)=
,设关于x的不等式f(x+a)<f(x)的解集为M,若[-
,
]⊆M,则实数a的取值范围是 .
|
| 1 |
| 2 |
| 1 |
| 2 |
考点:分段函数的应用
专题:计算题,数形结合,函数的性质及应用,不等式的解法及应用
分析:由题意可得,在[-
,
]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方.当a=0或 a>0时,检验不满足条件.当a<0时,应有f(-
+a)<f(-
),化简可得 a2-a-1<0,解得
<a<
,由此求得a的范围.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
1-
| ||
| 2 |
1+
| ||
| 2 |
解答:
 解:由于f(x)=
解:由于f(x)=
,
关于x的不等式f(x+a)<f(x)的解集为M,若[-
,
]⊆M,
则在[-
,
]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方.
当a=0时,显然不满足条件.
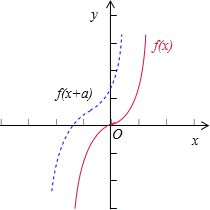
当a>0时,函数y=f(x+a)的图象是把函数y=f(x)的图象向左平移
a个单位得到的,
结合图象(右上方)可得不满足函数y=f(x+a)的图象在函数
y=f(x)的图象下方.
当a<0时,如图所示,要使在[-
,
]上,
函数y=f(x+a)的图象在函数y=f(x)的图象的下方,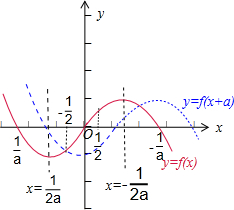
只要f(-
+a)<f(-
)即可,
即-a(-
+a)2+(-
+a)<-a(-
)2-
,
化简可得 a2-a-1<0,解得
<a<
,
故此时a的范围为(
,0).
综上可得,a的范围为(
,0),
故答案为:(
,0).
 解:由于f(x)=
解:由于f(x)=
|
关于x的不等式f(x+a)<f(x)的解集为M,若[-
| 1 |
| 2 |
| 1 |
| 2 |
则在[-
| 1 |
| 2 |
| 1 |
| 2 |
当a=0时,显然不满足条件.
当a>0时,函数y=f(x+a)的图象是把函数y=f(x)的图象向左平移
a个单位得到的,
结合图象(右上方)可得不满足函数y=f(x+a)的图象在函数
y=f(x)的图象下方.
当a<0时,如图所示,要使在[-
| 1 |
| 2 |
| 1 |
| 2 |
函数y=f(x+a)的图象在函数y=f(x)的图象的下方,

只要f(-
| 1 |
| 2 |
| 1 |
| 2 |
即-a(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
化简可得 a2-a-1<0,解得
1-
| ||
| 2 |
1+
| ||
| 2 |
故此时a的范围为(
1-
| ||
| 2 |
综上可得,a的范围为(
1-
| ||
| 2 |
故答案为:(
1-
| ||
| 2 |
点评:本题考查函数的单调性、二次函数的性质、不等式等知识,考查数形结合思想、分类讨论思想,考查学生分析解决问题的能力,注意排除法在解决选择题中的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若函数f(x)的定义域为[2,16],则y=f(x)+f(2x)的定义域为( )
| A、[2,16] |
| B、[1,8] |
| C、[1,16] |
| D、[2,8] |
将自然数1,2,3,…,n,…按第k组含k个数的规则分组:(1),(2,3),(4,5,6),…那么2012所在的组是( )
| A、第64组 | B、第63组 |
| C、第62组 | D、第61组 |