题目内容
被两条直线
x-y=1,y=-x-3截得的线段中点是P(0,3)的直线l的方程 .
| 1 |
| 2 |
考点:待定系数法求直线方程
专题:直线与圆
分析:取直线y=-x-3上的任意一点M(x,y),则M关于P(0,3)的中心对称点为N(-x,6-y).点N在直线
x-y=1上,可得x-2y+14=0,联立
,解得M(-
,
).再利用点斜式即可得出.
| 1 |
| 2 |
|
| 20 |
| 3 |
| 11 |
| 3 |
解答:
解:取直线y=-x-3上的任意一点M(x,y),则M关于P(0,3)的中心对称点为N(-x,6-y).
点N在直线
x-y=1上,∴
(-x)-(6-y)=1,化为x-2y+14=0,
∴
,解得
,M(-
,
).
∴kl=
=-
.
∴直线l的方程为:y=-
x+3.
故答案为:y=-
x+3.
点N在直线
| 1 |
| 2 |
| 1 |
| 2 |
∴
|
|
| 20 |
| 3 |
| 11 |
| 3 |
∴kl=
| ||
-
|
| 1 |
| 10 |
∴直线l的方程为:y=-
| 1 |
| 10 |
故答案为:y=-
| 1 |
| 10 |
点评:本题考查了中心对称性、中点坐标公式、点斜式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
若用m,n表示两条不同的直线,用α表示一个平面,则下列命题正确的是( )
| A、若m∥n,n?α,则m∥α |
| B、若m∥α,n?α,则m∥n |
| C、若m⊥n,n?α,则m⊥α |
| D、若m⊥α,n?α,则m⊥n |
若f(x)是定义在R上的增函数,则对任意x、y∈R,“f(x)+f(y)<f(-x)+f(-y)”是“x+y<0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
设扇形的弧长为2,面积为2,则扇形中心角的弧度数是( )
| A、1 | B、4 | C、1或4 | D、π |
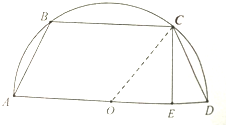 在半径为1的半圆中,作如图所示的等腰梯形ABCD,CE垂直下底AD于E,设DE=x(0<x<1),CE=h,梯形ABCD的周长为L.
在半径为1的半圆中,作如图所示的等腰梯形ABCD,CE垂直下底AD于E,设DE=x(0<x<1),CE=h,梯形ABCD的周长为L.