题目内容
9.已知数列{an},{bn}中,a1=2,b1=1,当n≥2时,an-an-1=1,$\frac{{b}_{n}}{{b}_{n-1}}$=2.(1)求数列{an},{bn}的通项公式;
(2)若cn=$\frac{1}{{a}_{n}{a}_{n+1}}$+(-n)•bn,求{cn}的前n项和.
分析 (1)运用等差数列和等比数列的定义和通项公式即可得到所求通项公式;
(2)cn=$\frac{1}{{a}_{n}{a}_{n+1}}$+(-n)•bn=$\frac{1}{(n+1)(n+2)}$+(-n)•2n-1=$\frac{1}{n+1}$-$\frac{1}{n+2}$+(-n)•2n-1;运用数列的求和方法:分组求和和裂项相消求和以及错位相减法,结合等比数列的求和公式,化简整理,即可得到所求和.
解答 解:(1)数列{an},{bn}中,a1=2,b1=1,
当n≥2时,an-an-1=1,$\frac{{b}_{n}}{{b}_{n-1}}$=2.
可得{an}为首项为2,公差为1的等差数列,
可得an=2+n-1=n+1;
可得{bn}为首项为1,公差为2的等比数列,
可得bn=2n-1;
(2)cn=$\frac{1}{{a}_{n}{a}_{n+1}}$+(-n)•bn=$\frac{1}{(n+1)(n+2)}$+(-n)•2n-1
=$\frac{1}{n+1}$-$\frac{1}{n+2}$+(-n)•2n-1;
则{cn}的前n项和为$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n+1}$-$\frac{1}{n+2}$+[(-1)•20+(-2)•21+…+(-n)•2n-1],
令Tn=(-1)•20+(-2)•21+…+(-n)•2n-1,
2Tn=(-1)•21+(-2)•22+…+(-n)•2n,
两式相减可得-Tn=-1+(-1)(21+…+2n-1)-(-n)•2n
=-1-$\frac{2(1-{2}^{n-1})}{1-2}$-(-n)•2n,
可得Tn=(1-n)•2n-1,
则{cn}的前n项和为$\frac{1}{2}$-$\frac{1}{n+2}$+(1-n)•2n-1=-$\frac{1}{2}$-$\frac{1}{n+2}$+(1-n)•2n.
点评 本题考查等差数列和等比数列的定义、通项公式和求和公式的运用,考查数列的求和方法:分组求和和裂项相消求和以及错位相减法,考查化简整理的运算能力,属于中档题.

| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 60 | ||
| 不肥胖 | 10 | ||
| 合计 | 100 |
(2)是否有95%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
附:参考公式:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$
| P(x2≥x0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
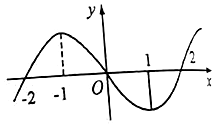 已知f(x)在R上是可导函数,f(x)的图象如图所示,则不等式f′(x)>0的解集为( )
已知f(x)在R上是可导函数,f(x)的图象如图所示,则不等式f′(x)>0的解集为( )| A. | (-2,0)∪(2,+∞) | B. | (-∞,2)∪(2,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-2,-1)∪(1,2) |
| A. | (-∞,1] | B. | (-∞,1) | C. | [1,+∞) | D. | (1,+∞) |
| A. | 66 | B. | 55 | C. | 44 | D. | 33 |
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 2 | 5 | 9 | 10 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 14 | 10 | 6 | 4 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 2 | 4 | 8 | 16 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | 6 | 6 | 3 |
(1)比较甲、乙两校学生的数学平均成绩的高低;
(2)若规定数学成绩不低于120分为优秀,从甲、乙两校全体高三学生中各随机抽取2人,其中数学成绩为优秀的共X人,求X的分布列及数学期望.
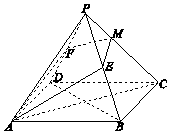 如图,在正四棱锥P-ABCD中,PA=AB,E,F分别为PB,PD的中点.
如图,在正四棱锥P-ABCD中,PA=AB,E,F分别为PB,PD的中点.