题目内容
14.已知函数$f(x)=\sqrt{3}sin({2ωx-\frac{π}{3}})+b(ω>0)$,且该函数图象的对称中心到对称轴的最小距离为$\frac{π}{4}$,当$x∈[{0,\frac{π}{3}}]$时,f(x)的最大值为1.(1)求函数f(x)的解析式;
(2)求f(x)的单调递增区间;
(3)若f(x)-3≤m≤f(x)+3在$[{0,\frac{π}{3}}]$上恒成立,求m的取值范围.
分析 (1)根据对称中心到对称轴的最小距离为$\frac{π}{4}$,可得周期T,从而求解ω,当$x∈[{0,\frac{π}{3}}]$时,求解出内层函数的范围,求解f(x)的最大值,令其等于1.求解b可得函数f(x)的解析式.
(2)将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;
(3)当$x∈[{0,\frac{π}{3}}]$时,f(x)的最大值为1.只需求解最小值,可得m的范围.
解答 解:(1)函数$f(x)=\sqrt{3}sin({2ωx-\frac{π}{3}})+b(ω>0)$,
∵对称中心到对称轴的最小距离为$\frac{π}{4}$,
∴周期T=4×$\frac{π}{4}=π$.
∴$\frac{2π}{2ω}=π$,
∴ω=1,
故得f(x)=$\sqrt{3}$sin(2x-$\frac{π}{3}$)+b
当$x∈[{0,\frac{π}{3}}]$上时,
2x-$\frac{π}{3}$∈[$-\frac{π}{3}$,$\frac{π}{3}$],
则sin(2x-$\frac{π}{3}$)∈[$-\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$]
∴f(x)的最大值为$\frac{3}{2}$+b=1,
∴b=$-\frac{1}{2}$.
那么:f(x)最小值为-2.
∴函数f(x)的解析式为f(x)=$\sqrt{3}$sin(2x-$\frac{π}{3}$)-$\frac{1}{2}$
(2)由$-\frac{π}{2}+2kπ≤$2x-$\frac{π}{3}$$≤\frac{π}{2}+2kπ$,k∈Z,
可得:$-\frac{π}{12}+kπ$≤x≤$\frac{π}{3}+kπ$.
f(x)的单调递增区间为[$-\frac{π}{12}+kπ$,$\frac{π}{3}+kπ$],k∈Z,
(3)由(1)可知当$x∈[{0,\frac{π}{3}}]$时,f(x)的最大值为1.最小值为-2.
f(x)-3≤m≤f(x)+3在$[{0,\frac{π}{3}}]$上恒成立,
即:-2-3≤m≤1+3,
可得:-5≤m≤4.
故得m的取值范围是[-5,4].
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,确定f(x)的解析式是解决本题的关键.属于中档题.

| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
| 得禽流感 | 不得禽流感 | 总计 | |
| 服药 | 5 | 45 | 50 |
| 不服药 | 14 | 36 | 50 |
| 总计 | 19 | 81 | 100 |
(Ⅱ)在服药后得禽流感的鸡中,有2只母鸡,3只公鸡,在这5只鸡中随机抽取3只再进行研究,求至少抽到1只母鸡的概率
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
临界值表
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | e | B. | 2e | C. | 1 | D. | 2 |
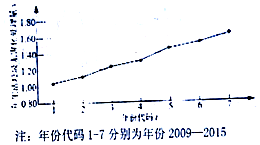 如图是我国2009年至2015年生活垃圾无害化处理量(单位:亿吨)的折线图
如图是我国2009年至2015年生活垃圾无害化处理量(单位:亿吨)的折线图