��Ŀ����
19��ij�����⽨��һ����������ݣ���ȡ����ķ�ʽ�Ӷ�ҽ�����˾ѡȡһ�ҽ�����˾���������ɸѡ���ס������ҽ�����˾���������б꣮�ִӽ������ԺƸ��ר�������һ���б귽�������ҹ�˾��6���б������������ȡ3�����⣬��֪��6���б������У���˾����ȷ�ش�����4����Ŀ�����ҹ�˾������ش�ÿ����Ŀ�ĸ��ʾ�Ϊ$\frac{2}{3}$���ס������ҹ�˾��ÿ��Ļش��������������Ӱ��ģ���1����ס������ҹ�˾�����2����Ŀ�ĸ��ʣ�
��2����������ͷ���ĽǶȷ������ס��������ļҹ�˾����ɹ��Ŀ����Ը���
���� ��1�����ö����ظ�����ĸ��ʹ�ʽ���ס������ҹ�˾�����2����Ŀ�ĸ��ʣ�
��2�����˾��ȷ������Ե�����ΪX����X��ȡֵ�ֱ�Ϊ1��2��3��������ʣ��õ�X�ķֲ�������������ҹ�˾��ȷ������Ե���ΪY����Yȡֵ�ֱ�Ϊ0��1��2��3��������ʵõ��ֲ��У�����������ɣ�
��� �⣺��1���������֪���������$P=\frac{C_4^1C_2^2}{C_6^3}��C_3^1{��{\frac{2}{3}}��^1}{��{1-\frac{2}{3}}��^2}+\frac{C_4^2C_2^1}{C_6^3}��{��{1-\frac{2}{2}}��^3}=\frac{1}{15}$��
��2�����˾��ȷ������Ե�����ΪX����X��ȡֵ�ֱ�Ϊ1��2��3.$P��{X=1}��=\frac{C_4^1C_2^2}{C_6^3}=\frac{1}{5}$��$P��X=2��=\frac{C_4^2C_2^1}{C_6^3}=\frac{3}{5}$��$P��{X=3}��=\frac{C_4^3C_2^0}{C_6^3}=\frac{1}{5}$��
��X�ķֲ���Ϊ��
| X | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
���ҹ�˾��ȷ������Ե���ΪY����Yȡֵ�ֱ�Ϊ0��1��2��3.$P��{Y=0}��=\frac{1}{27}$��$P��{Y=1}��=C_3^1��\frac{2}{3}��{��{\frac{1}{3}}��^2}=\frac{2}{9}$��$P��{Y=2}��=C_3^2��{��{\frac{2}{3}}��^2}��\frac{1}{3}=\frac{4}{9}$��$P��{Y=3}��={��{\frac{2}{3}}��^3}=\frac{8}{27}$
��Y�ķֲ���Ϊ��
| Y | 0 | 1 | 2 | 3 |
| P | $\frac{1}{27}$ | $\frac{2}{9}$ | $\frac{4}{9}$ | $\frac{8}{27}$ |
��E��X��=D��Y����D��X����D��Y���ɵã���˾����ɹ��Ŀ����Ը���
���� ���⿼������ظ���������Լ��ֲ������������������������

��ϰ��ϵ�д�
�����Ŀ
14����֪ԲM��ֱ��3x-4y=0��3x-4y+10=0�����У�Բ����ֱ��y=-x-4�ϣ���ԲM�ķ���Ϊ��������
| A�� | ��x+3��2+��y-1��2=1 | B�� | ��x-3��2+��y+1��2=1 | C�� | ��x+3��2+��y+1��2=1 | D�� | ��x-3��2+��y-1��2=1 |
11����֪˫���ߦ���$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$��a��0��b��0����һ��������Ϊl��ԲC����x-a��2+y2=8��l����A��B���㣬����ABC�ǵ���ֱ�������Σ���$\overrightarrow{OB}=5\overrightarrow{OA}$������OΪ����ԭ�㣩����˫���ߦ���������Ϊ��������
| A�� | $\frac{{\sqrt{13}}}{3}$ | B�� | $\frac{{2\sqrt{13}}}{3}$ | C�� | $\frac{{\sqrt{13}}}{5}$ | D�� | $\frac{{2\sqrt{13}}}{5}$ |
8��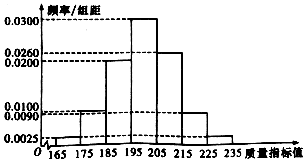 ij�ֲ�Ʒ��������������ָ�����������������ָ��ֵ���ֵȼ������
ij�ֲ�Ʒ��������������ָ�����������������ָ��ֵ���ֵȼ������
��ij��ҵ���������ֲ�Ʒ�г�ȡ200��������õ����µ�Ƶ�ʷֲ�ֱ��ͼ��
��1���������ϳ�����������ݣ��ܷ���Ϊ����ҵ�������ֲ�Ʒ���ϡ�һ������Ʒ����Ҫռ��ȫ����Ʒ��92%�Ĺ涨����
��2���������У�����Ʒ�ȼ��÷ֲ�����ķ�����ȡ8�����ٴ���8����Ʒ�������ȡ4�������ȡ��4����Ʒ�У�һ����������Ʒ���еĸ��ʣ�
��3������ҵΪ��߲�Ʒ����������չ�ˡ����������¡��������ٳ�����⣬��Ʒ����ָ��ֵX��������X��N��218��140���������������¡���������ָ��ֵ�ľ�ֵ�Ȼǰ��Լ�����˶��٣�
 ij�ֲ�Ʒ��������������ָ�����������������ָ��ֵ���ֵȼ������
ij�ֲ�Ʒ��������������ָ�����������������ָ��ֵ���ֵȼ������| ����ָ��ֵm | m��185 | 185��m��205 | M��205 |
| �ȼ� | ����Ʒ | ����Ʒ | һ��Ʒ |
��1���������ϳ�����������ݣ��ܷ���Ϊ����ҵ�������ֲ�Ʒ���ϡ�һ������Ʒ����Ҫռ��ȫ����Ʒ��92%�Ĺ涨����
��2���������У�����Ʒ�ȼ��÷ֲ�����ķ�����ȡ8�����ٴ���8����Ʒ�������ȡ4�������ȡ��4����Ʒ�У�һ����������Ʒ���еĸ��ʣ�
��3������ҵΪ��߲�Ʒ����������չ�ˡ����������¡��������ٳ�����⣬��Ʒ����ָ��ֵX��������X��N��218��140���������������¡���������ָ��ֵ�ľ�ֵ�Ȼǰ��Լ�����˶��٣�
9����֪����{an}������ƹ�ϵ��an+1=$\frac{{a}_{n}}{{a}_{n}+1}$��a1=$\frac{1}{2}$����a2017=��������
| A�� | $\frac{1}{2016}$ | B�� | $\frac{1}{2017}$ | C�� | $\frac{1}{2018}$ | D�� | $\frac{1}{2019}$ |